Lecture1

Exercises

Exercises

1. Run the edit distance algorithm from the slides on s=“GO”, t=“LOG”:  look down

   • What is the edit distance? What edit operations does the algorithm suggest? Insert, nothing, replace nothing 2
   • Draw the recursion tree for a memoized version of the algorithm. 
   • Count and compare how many recursive calls are made by the memoized algorithm and how many by a recursive algorithm without memoization.

2. Answer questions 2 and 3 below the videos (see above).

   1. There is an error in the Dynamic Programming 2 video: something is missing in CoinChange2M pseudocode. What is it?
   2. In both videos, how much space used by the algorithms can be reduced, if you are not required to print the chosen coins, just the optimal number of them?

3. Based on the slides, write a pseudocode of a dynamic programming algorithm for the activity selection problem (using the first recurrence, see slide 31). First, write an algorithm to return the maximum number of activities. Then, augment it to print out the selected activities.

4. Solve CLRS4 14-2 (CLRS3 15-2), if you have time.  Follow the roadmap presented today. First, write a recurrence, then an algorithm to find the length of the longest palindrome. Finally, augment the algorithm to return the longest palindrome itself.

task1

a)

			G	O
	j/i	0	1	2
	0	0	1D	2D
L	1	1I	1R	2R
O	2	2I	2R	1C
G	3	3I	2C	2I
Costs:

• insert = 1 = I
• delete = 1 = D
• replace = 1 (yes this is right it is the same as delete and insert) = R
• do nothing = 0 = C

b)

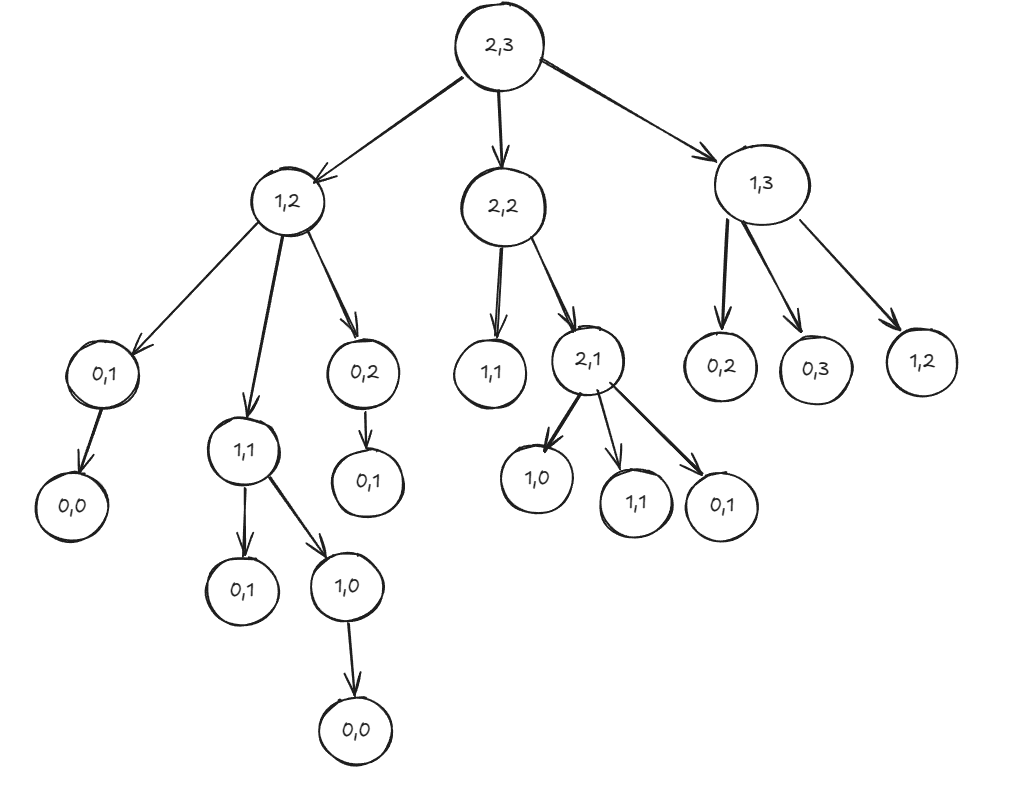
task3

def activitySelection(start, finish):
	timeformat = []
	for x in range(len(start)):
		timeformat.append((finish[x], start[x]))
		
	timeformat.sort()
 
	lastsave = 0
	count = 0
 
	for x in timeformat:
		if x[1] >= lastsave:
			lastsave = x[0]
			count = count + 1
			print(x[1], x[0])
	
	return count
 
	
	
 
 
 
start = [1, 3, 0, 5, 8, 5]
finish = [2, 4, 6, 7, 9, 9]
print(activitySelection(start, finish))
 
 
 
 
 

2