Lecture10

1. Computable
   1. If the input does not encode a DTM (this can be done by a halting DTM as argued in the lecture), then reject.
   2. Otherwise, the input is of the form ⌜M ⌝. In particular, the input starts with a prefix 1n# where n ∈ N is the number of states of M .
   3. If n is greater than 5, then accept; otherwise, reject. (This can be determined by checking that the first six letters of the input are all 1’s.)
2. Is computable. we know that anything under 1001 steps accepts, so it halts.
3. Since it just says finite steps, we dont actually know when, and it is like AP
4. 

So essentially when you find a non x, delete it, find an x, delete that, and repeat. this should halt and is computable.

We assume that AP is not computable. So if its compliment would be computably-enumerable, that would make AP itself computable, which is obviously not correct.

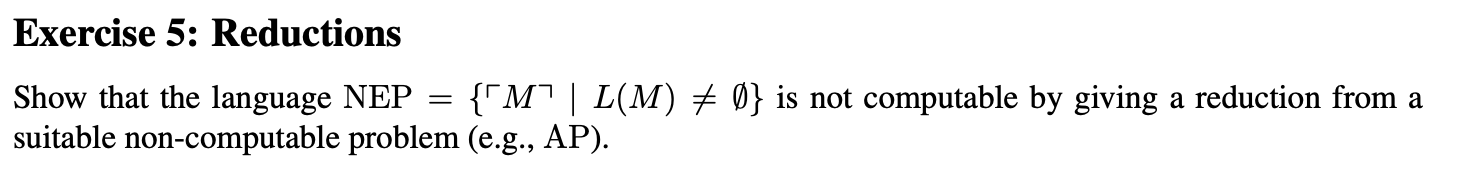
If you take the compliment of NEP then it will always accept on an empty and never on anything else.