- Run the Huffman algorithm and encode the example string on slide 20. Then, solve CLRS4 15.3-3 (CLRS3 16.3-3). By how much the text with the frequencies of characters as given in the exercise would be compressed?
- Consider a graph with eight vertices numbered from 1 to 8 and the following edges (given in the format (vertex1, vertex2; weight)): (5, 8; 1), (5, 6; 2), (1, 2; 3), (4, 6; 4), (4, 5; 5), (3, 4; 6), (4, 8; 7), (6, 7; 8), (5, 7; 9), (3, 7; 10), (2, 7; 11), (1, 8; 12). Show which edges belong to a partially completed MST after 7 iterations of Prim’s algorithm (use vertex 5 as a starting vertex).
- Solve CLRS4 21.1-2 (CLRS3 23.1-2). welp guess its too hard.
- Solve CLRS4 15.2-5 (CLRS3 16.2-5). Prove your greedy choice property. what the fuck am i supposed to do?
- Solve CLRS4 15.1-4 (CLRS3 16.1-4). Argue that your algorithm correctly finds an optimal solution. (Hint: Prove by contradiction. Assume that the algorithm’s solution with k lecture halls is not optimal and the k-th lecture hall is not necessary, then, investigate the first activity scheduled in this lecture hall.) (The exercise formulation ends with a paragraph in parentheses that maps the problem to an interval graph problem. While this is interesting, it is a bit of a distraction as just building such a graph would be more expensive than the running time of an algorithm that you should propose.) this one as well
oho ho, ole o3 h2 l1 1e
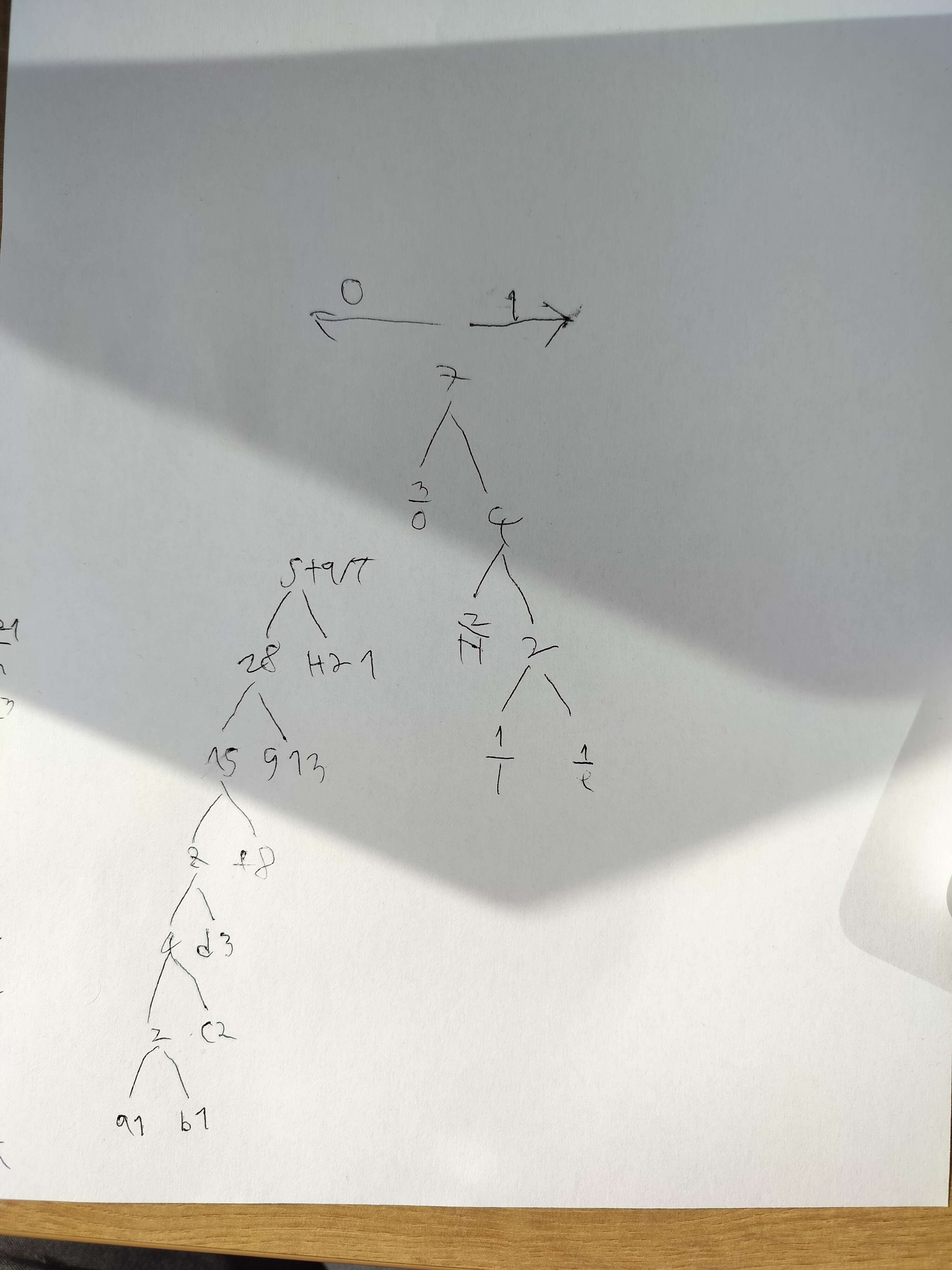when its fibanachi it grows linealy because as you can see, it is a long path instead of a more tree like structure.
well this is 8 itterations, but just ditch the one.
