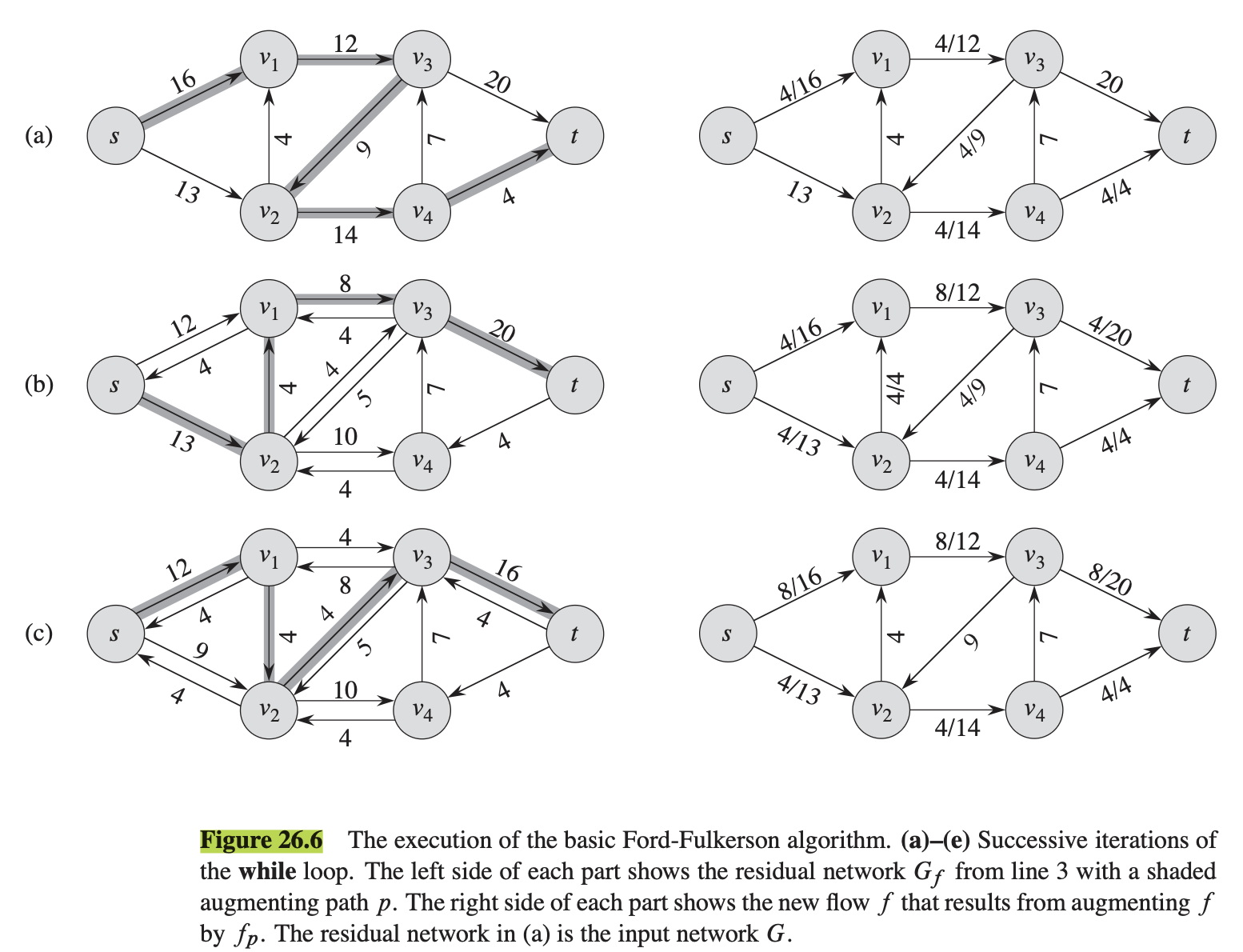
- Run the Edmonds-Karp algorithm on the example on slide 21. Start with the augmenting path sadt. Show each augmenting path used and the corresponding residual network. How many augmenting paths do you use? What are their lengths? Does flow cancellation happen in the example? If yes, when?
- Solve CLRS4 24.2-4, 24.1-7 (CLRS3 26.2-4, 26.1-7).
- Solve CLRS4 24.1-6 (CLRS3 26.1-6) (Requires some creativity, but try to see what ideas you can generate. The hardest problem is to prevent both children from going through the same street in opposite directions. This can be solved by transforming each edge of the flow network into something that has more edges…)
- Solve CLRS4 29.2-5. (CLRS3 29.2-6). Formulate a binary linear program (decision variables are required to be either 0 or 1).
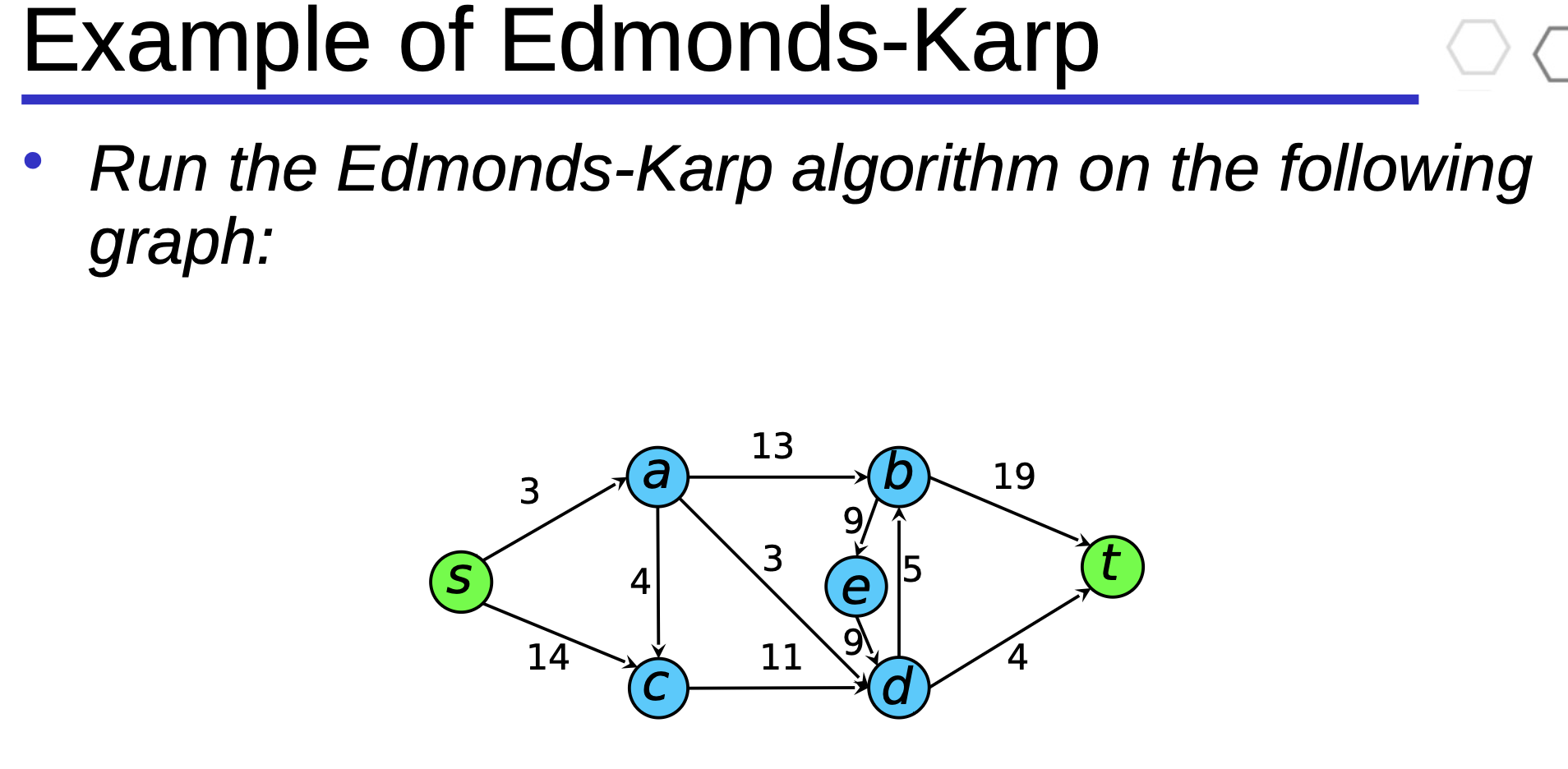
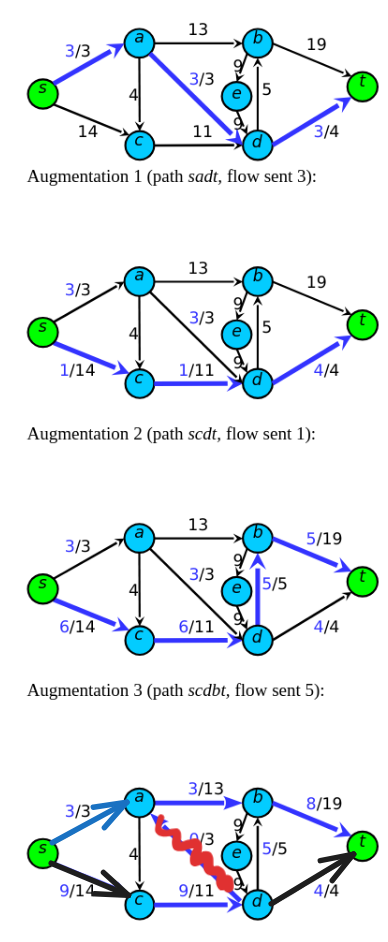
so the last step is just where we realize that we are being stinky poopie heads and can do it more efficiently by ditching the a-d line in favor of the top path, and then in the same picture (the last one) he fills up the bottom path as well. so its essentially 2 steps in 1.
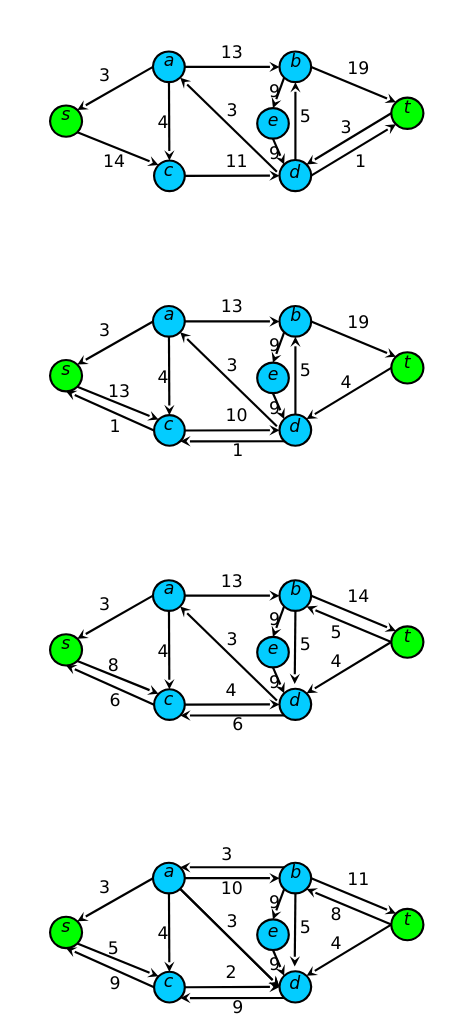 2)
2)

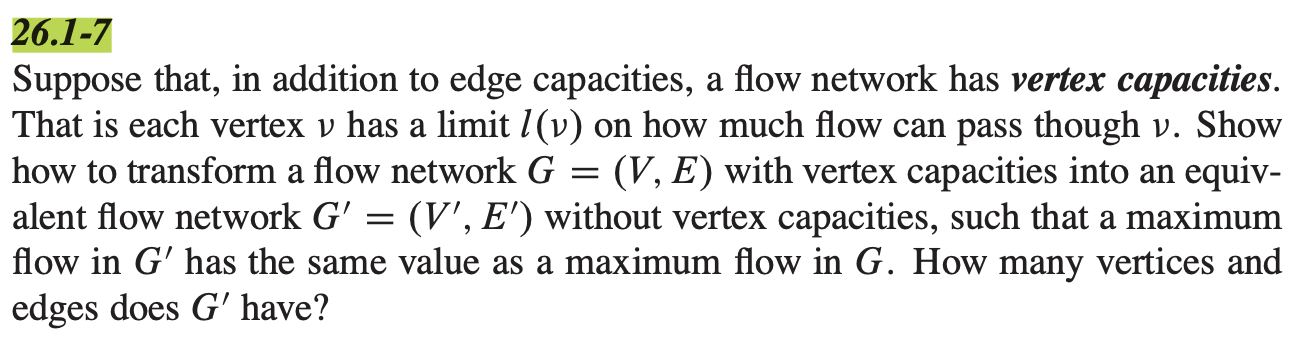
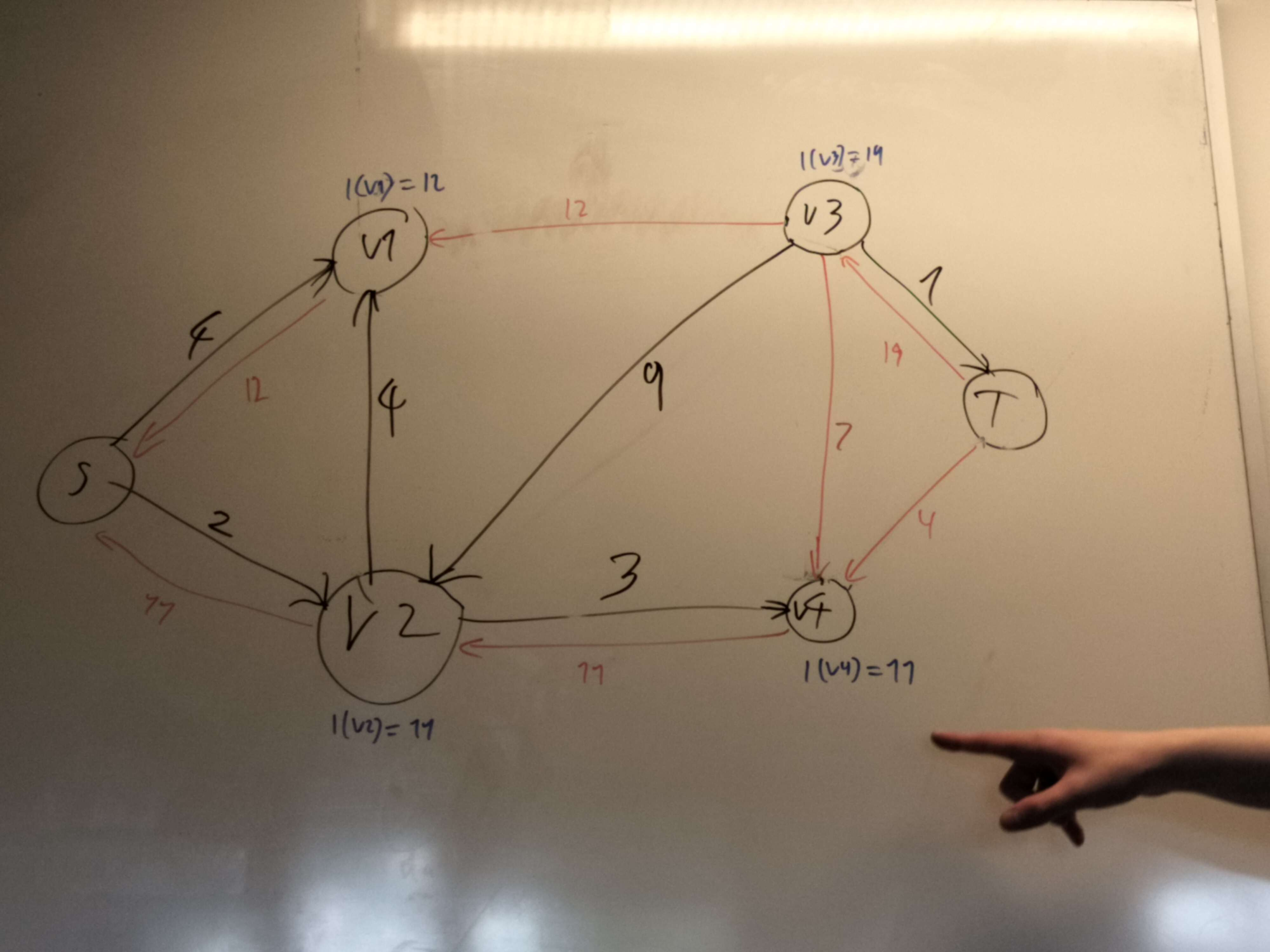
hey look if our limits are high enough then it doesnt matter. So just set limits to whatever your flow is and then its equivilant.