Quartz 4

Session 10 Continuous Systems part 1

3 min read

Exercises

  • We study the syntax and semantics of the continuous-time model
  • We show how to model continuous systems using differential equations.
  • We study how to solve differential equations numerically.
  • We define the notion of stability.

Exercise 1

a)

def euler_method (f , x0 , h , N ):
	x[0] = x0
	for i in range(N):
		print(x[i])
		x[i + 1] = x[i] + h * f(x[i])
	return x

b) 

 
def euler_method(f, x0, t0, h, N):
    # Initialize arrays to store results
    x = [0] * (N + 2)
    t = [0] * (N + 2)
 
    # Set initial conditions
    x[0] = x0
    t[0] = t0
 
    # Perform Euler method iterations
    for i in range(N + 1):
        print(x[i])  # Print current value of x
        t[i + 1] = t[i] + h  # Update time
        x[i + 1] = x[i] + h * f(x[i], t[i])  # Update x using Euler formula
 
    return t, x
 
def f(x, t):
    return t  # The function dx/dt = t
 
# Example call
t, x = euler_method(f, 0, 0, 1, 5)

What is an ODE (ODEs) c)

So this is correct because our x0 variable is just whatever input variables we can give it, it is not the order of anything, it is just the input variables. Example 1,3,5 where 1 is the speed, 3 is the drag, and 5 is acceleration.

 
def euler_method(f, x0, t0, h, N):
    # Initialize arrays to store results
    x = [0] * (N + 2)
    t = [0] * (N + 2)
 
    # Set initial conditions
    x[0] = x0[0]
    t[0] = t0
 
    # Perform Euler method iterations
    for i in range(N + 1):
        print(x[i])  # Print current value of x
        t[i + 1] = t[i] + h  # Update time
        x[i + 1] = x[i] + h * f(x[i], t[i])  # Update x using Euler formula
 
    return t, x
 
def f(x, t):
    return t  # The function dx/dt = t
 
# Example call
t, x = euler_method(f, [1], 0, 1, 8)

D)

Exercise 2

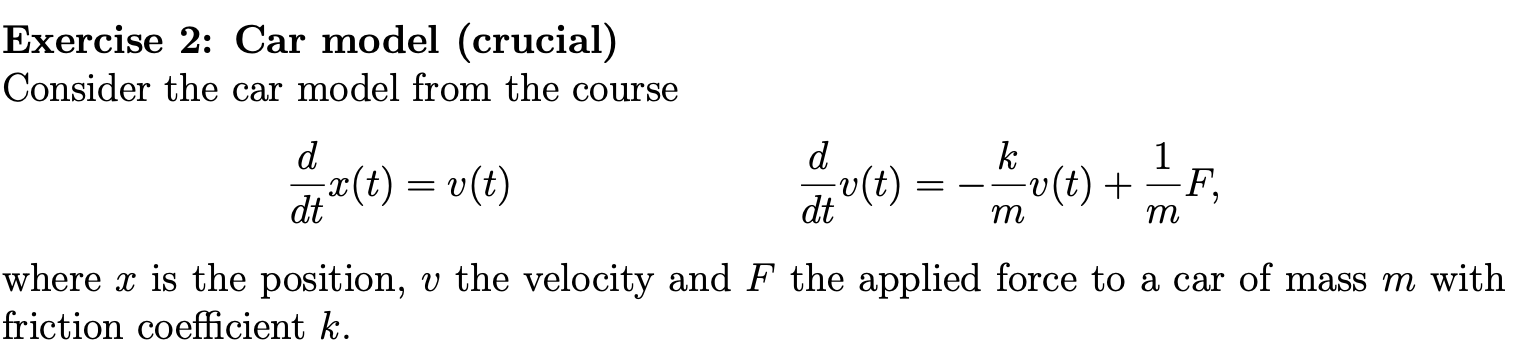
B)

def euler_method(f, x0, t0, h, N):
    # Initialize arrays to store results
    # x will be a list of vectors, each containing [position, velocity]
    x = [None] * (N + 2)
    t = [0] * (N + 2)
 
    # Set initial conditions
    x[0] = x0.copy()  # Store the full initial state vector
    t[0] = t0
 
    # Perform Euler method iterations
    for i in range(N + 1):
        print(f"Step {i}: position = {x[i][0]:.3f}, velocity = {x[i][1]:.3f}")
        t[i + 1] = t[i] + h  # Update time
 
        # Get derivatives from f function
        derivatives = f(x[i], t[i])
 
        # Update state vector using Euler formula
        x[i + 1] = [x[i][j] + h * derivatives[j] for j in range(len(x[i]))]
 
    return t, x
 
def f(x, t):
    F = 1000      # Applied force
    m = 1000     # Mass
    k = 50       # Damping coefficient
 
    # x[0] is position, x[1] is velocity
    der_x = x[1]                           # dx/dt = velocity
    der_v = -k/m * x[1] + F/m             # dv/dt = acceleration
 
    return [der_x, der_v]
 
# Example call with initial position=1, initial velocity=0
t, x = euler_method(f, [1, 0], 0, 1, 88)
 
# Print final results
print("\nFinal Results:")
for i in range(len(t)-1):  # -1 because we have N+2 elements but only N+1 are used
    print(f"t[{i}] = {t[i]}, position = {x[i][0]:.3f}, velocity = {x[i][1]:.3f}")

Exercise 3

Exercise 4

Exercise 5

Graph View

Backlinks