Session 11 Continuous Systems part 2

a

 
 
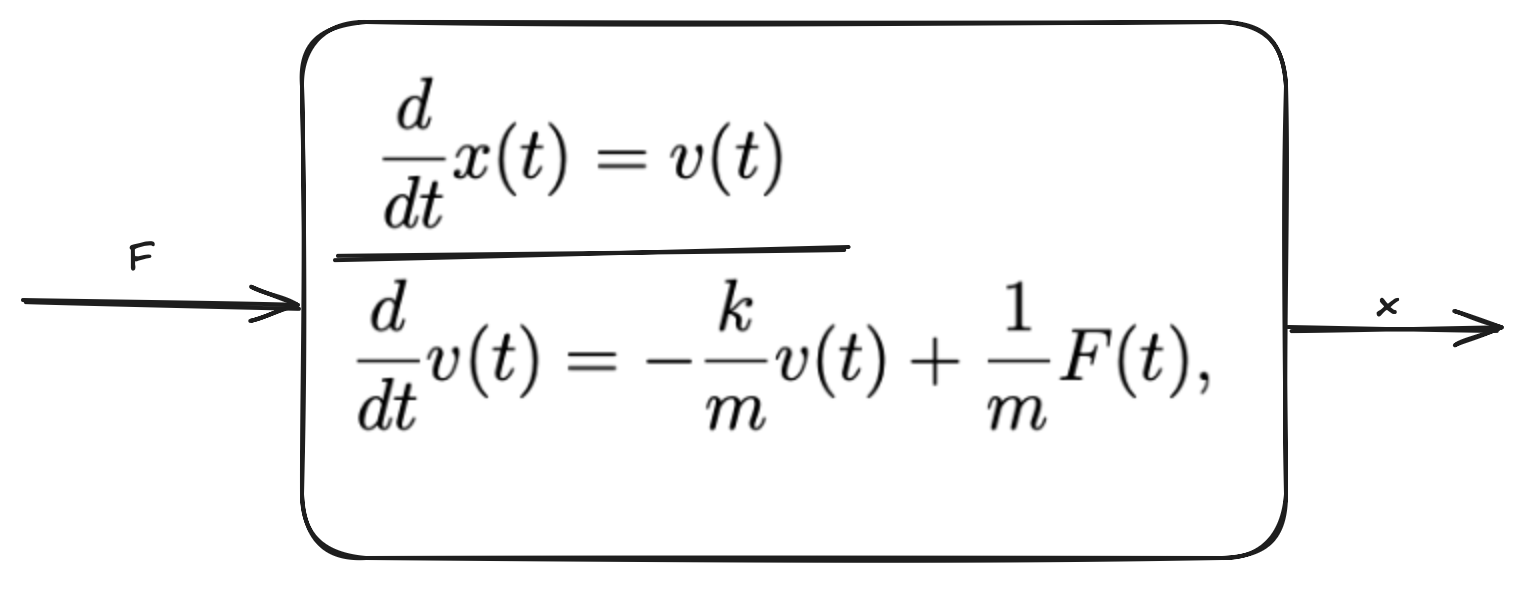
fn main() {
    // Define the derivative function: dx/dt = t
    /* let f = |x: &[f64], t: f64| -> Vec<f64> {
        vec![t] // Ignores x
    }; */
 
    let f = |x: &[f64], t: f64| -> Vec<f64> {
        let m = 1000.0;
        let k = 50.0;
        let kp = 3.3;
        let r = 0.0;
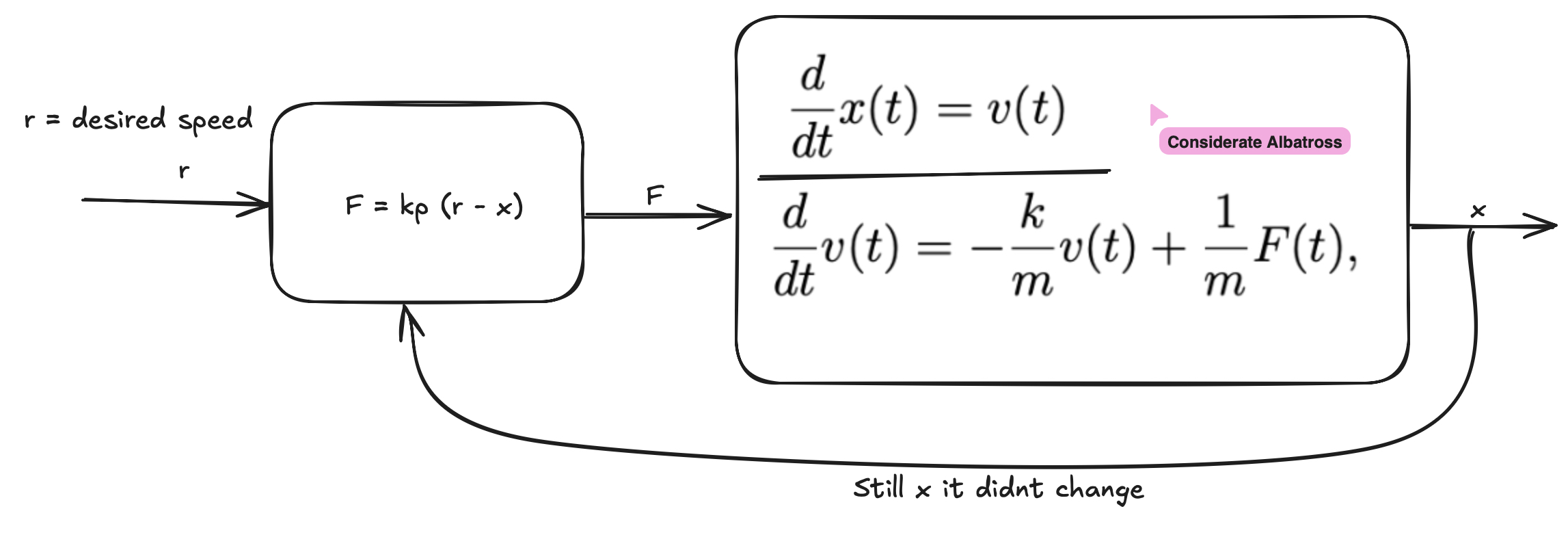
        let der_x = x[1];
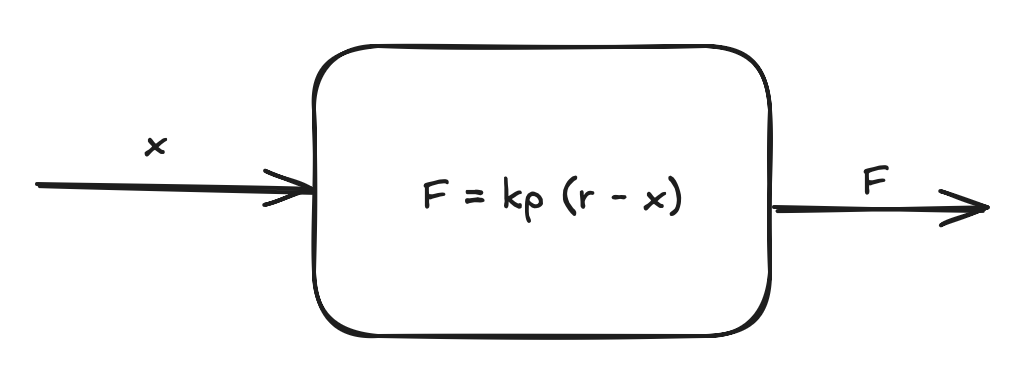
        let der_v = -k / m * x[1] + kp * (r - x[0]) / m;
        vec![der_x, der_v]
    };
 
    let t0 = 0.0;
    let x0 = vec![100.0, 0.0]; // Initial condition x(0) = 0
    let h = 0.5;
    let n = 1000;
 
    let (t, result) = runge_kutta_4(f, &x0, t0, h, n);
 
    // Print the solution at each step
    for (time, state) in t.iter().zip(result.iter()) {
        println!("t = {:.1}, x = {:.6}", time, state[0]);
    }
}
 
pub fn runge_kutta_4<F>(f: F, x0: &[f64], t0: f64, h: f64, n: usize) -> (Vec<f64>, Vec<Vec<f64>>)
where
    F: Fn(&[f64], f64) -> Vec<f64>,
{
    let mut t = vec![t0];
    let mut result = vec![x0.to_vec()];
 
    for _ in 0..n {
        let xi = &result[result.len() - 1];
        let ti = t[t.len() - 1];
 
        let k1 = f(xi, ti);
        let k2 = f(&extend(xi, h / 2.0, &k1), ti + h / 2.0);
        let k3 = f(&extend(xi, h / 2.0, &k2), ti + h / 2.0);
        let k4 = f(&extend(xi, h, &k3), ti + h / 2.0);
 
        let mut next_x = Vec::with_capacity(xi.len());
        for j in 0..xi.len() {
            let step = xi[j] + (h / 6.0) * (k1[j] + 2.0 * k2[j] + 2.0 * k3[j] + k4[j]);
            next_x.push(step);
        }
 
        result.push(next_x);
        t.push(ti + h);
    }
 
    (t, result)
}
 
fn extend(x: &[f64], h: f64, der: &[f64]) -> Vec<f64> {
    assert_eq!(x.len(), der.len());
    x.iter()
        .zip(der.iter())
        .map(|(&xj, &derj)| xj + h * derj)
        .collect()
}

 
 
fn main() {
    // Define the derivative function: dx/dt = t
    /* let f = |x: &[f64], t: f64| -> Vec<f64> {
        vec![t] // Ignores x
    }; */
 
let f = |x: &[f64], t: f64| -> Vec<f64> {
        let m = 1000.0;
        let k = 50.0;
        let kp = 20.0;
        let kd = 200.0;
        let r = 0.0;
        let f = kp * (r - x[0]) - kd * x[1];
        let der_x = x[1];
        let der_v = -k / m * x[1] + f / m;
        vec![der_x, der_v]
    };
    let t0 = 0.0;
    let x0 = vec![100.0, 0.0]; // Initial condition x(0) = 0
    let h = 0.5;
    let n = 1000;
 
    let (t, result) = runge_kutta_4(f, &x0, t0, h, n);
 
    // Print the solution at each step
    for (time, state) in t.iter().zip(result.iter()) {
        println!("t = {:.1}, x = {:.6}", time, state[0]);
    }
}
 
pub fn runge_kutta_4<F>(f: F, x0: &[f64], t0: f64, h: f64, n: usize) -> (Vec<f64>, Vec<Vec<f64>>)
where
    F: Fn(&[f64], f64) -> Vec<f64>,
{
    let mut t = vec![t0];
    let mut result = vec![x0.to_vec()];
 
    for _ in 0..n {
        let xi = &result[result.len() - 1];
        let ti = t[t.len() - 1];
 
        let k1 = f(xi, ti);
        let k2 = f(&extend(xi, h / 2.0, &k1), ti + h / 2.0);
        let k3 = f(&extend(xi, h / 2.0, &k2), ti + h / 2.0);
        let k4 = f(&extend(xi, h, &k3), ti + h / 2.0);
 
        let mut next_x = Vec::with_capacity(xi.len());
        for j in 0..xi.len() {
            let step = xi[j] + (h / 6.0) * (k1[j] + 2.0 * k2[j] + 2.0 * k3[j] + k4[j]);
            next_x.push(step);
        }
 
        result.push(next_x);
        t.push(ti + h);
    }
 
    (t, result)
}
 
fn extend(x: &[f64], h: f64, der: &[f64]) -> Vec<f64> {
    assert_eq!(x.len(), der.len());
    x.iter()
        .zip(der.iter())
        .map(|(&xj, &derj)| xj + h * derj)
        .collect()
}