4 A External-memory algorithms general principles and the multiway merge-sort algorithm

Key Points

1. Why External Memory?

   • Data too large for RAM → stored on disk (HDD/SSD).
   • Disk I/O is slow: Random accesses are expensive; sequential accesses are better.
   • Goal: Minimize I/O operations (read/write blocks of size B).

2. General Principles:

   • I/O Complexity: Measure performance in number of disk block transfers.
   • B-Trees: Balanced search trees optimized for disk (high branching factor).
   • Multiway Merge-Sort: External sorting algorithm that minimizes I/O.

3. Multiway Merge-Sort:

   • Phases:
     1. Split: Divide data into chunks that fit in memory (M = memory size).
     2. Sort: Sort each chunk in memory.
     3. Merge: Merge sorted chunks using a k-way merge (where k ≈ M/B).
   • I/O Complexity: $$O\left(\frac{N}{B}{\log }_{\frac{M}{B}}\frac{N}{M}\right)$$ where N = total data size, B = block size, M = memory size.

Example: Multiway Merge-Sort

• Input: Large unsorted data (e.g., 100 GB).

• Steps:

  1. Split data into chunks of size M (e.g., 1 GB chunks if M = 1 GB).
  2. Sort each chunk in RAM → write sorted runs to disk.
  3. Merge runs in passes:
     • Each pass merges k runs into one larger run.
     • Repeat until one sorted run remains.

• Visualization:
  
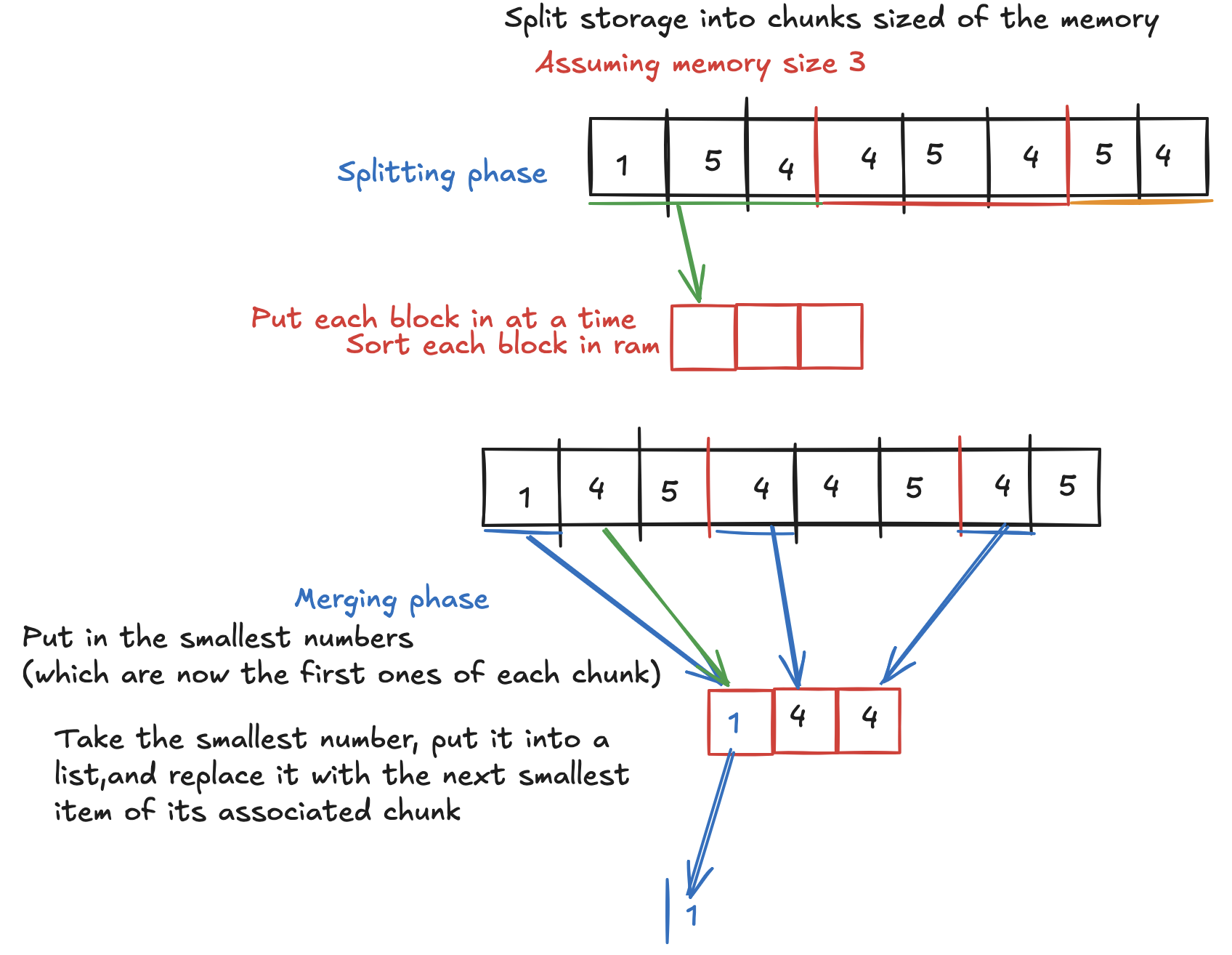
  Diagram shows:

  • Initial splits → sorted runs (R₁, R₂, …).
  • k-way merge producing larger runs.
  • Final merged output.

Presentation Order

1. Motivation (1 min):

   • “Disks are slow for random I/O. External-memory algorithms optimize for sequential block accesses.”
   • Compare RAM (random access) vs. disk (sequential preferred).

2. Multiway Merge-Sort Steps (2 mins):

   • “Split data into memory-sized chunks, sort each chunk, then merge them in passes.”
   • Sketch the diagram on the board and walk through phases.

3. I/O Complexity (1 min):

   • “Complexity is logarithmic in N, but base is M/B (large → fewer passes).”
   • Example: If M = 1 GB, B = 4 KB, then k ≈ 250,000-way merge!

---