Key Points
- Formal Languages:
- A formal language is a set of strings over an alphabet (e.g., Σ = {0, 1}).
- Example: L = {w ∈ {0, 1}* | w ends with 0}.
Machine behaviour: scan all the way to the right end of the input, then check the last symbol.
| State | 1 | 0 | blank | Meaning |
|---|---|---|---|---|
| q1 | (q1, 1, R) | (q1, 0, R) | (q2, □, L) | Scan rightward |
| q2 | (q_rej, 1, –) | (q_acc, 0, –) | (q_rej, □, –) | Check last symbol |
- q_acc – accept (halt)
- q_rej – reject (halt)
-
Turing Machines (TMs):
- Deterministic TM (DTM):
- Defined by states Q, tape alphabet Γ, transition function δ.
- At each step, exactly one move is possible.
- Non-Deterministic TM (NTM):
- δ allows multiple choices per state/symbol pair.
- Accepts if any computation path leads to acceptance.
- Multi-Tape TM:
- Multiple tapes (e.g., input, work, output).
- Equivalent to single-tape TMs (Church-Turing thesis). Since you can just simulate multiple tapes
- Deterministic TM (DTM):
-
Church-Turing Thesis:
- “Any algorithmically computable function can be computed by a Turing machine.”
- Supported by equivalence of TMs, λ-calculus, and modern programming languages.
-
Halting Problem:
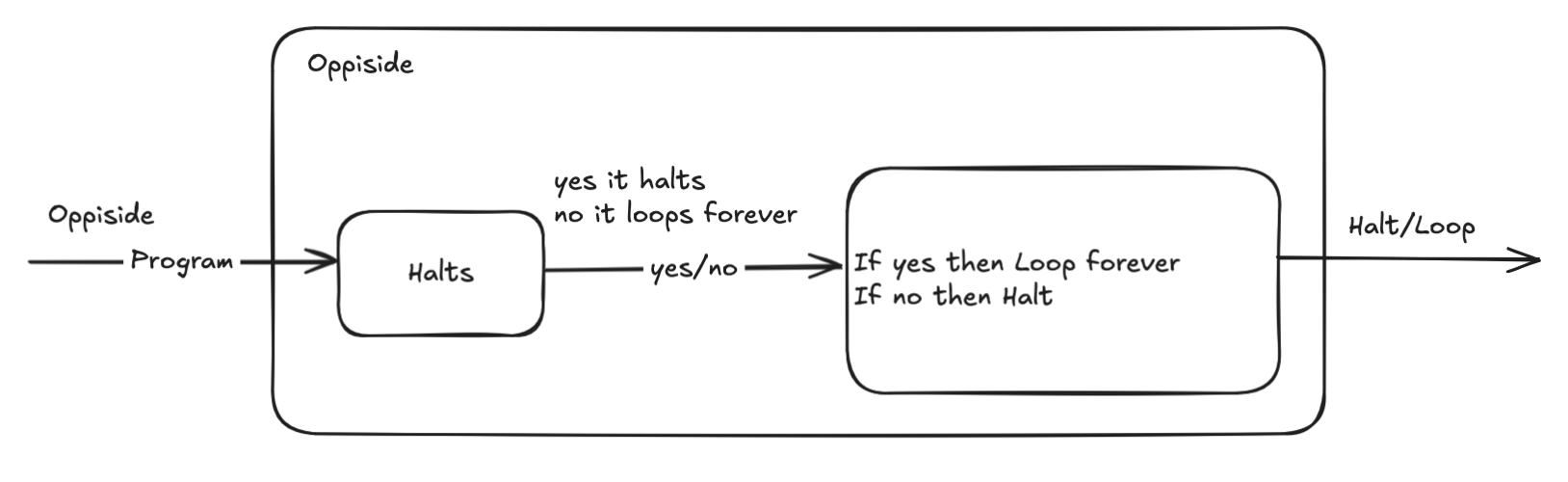
-
Closure Properties:
- Computable languages are closed under:
- Union, intersection, complement, concatenation, Kleene star.
- Computably-enumerable (c.e.) languages are closed under:
- Union, intersection, concatenation (but not complement). Because the complement of HALT is not Computably-enumerable).
- Computable languages are closed under:
Presentation Order
-
Formal Languages & TMs (1.5 mins):
- Define formal languages and TM variants (DTM/NTM/multi-tape).
- “TMs capture all computable functions (Church-Turing thesis).”
-
Halting Problem (1.5 mins):
- State HP and its uncomputability.
- Sketch the diagonalization proof (use blackboard).
-
Closure Properties (1 min):
- List key closures for computable/c.e. languages.
- “C.e. languages are not closed under complement (e.g., HP).”