Mtcps Exam

todo:

• hybrid models
• Derive pid (more training)
• Linear model (being able to make one)
• Have an example of stability for explaining the concept of stability
• Understand cruise controller

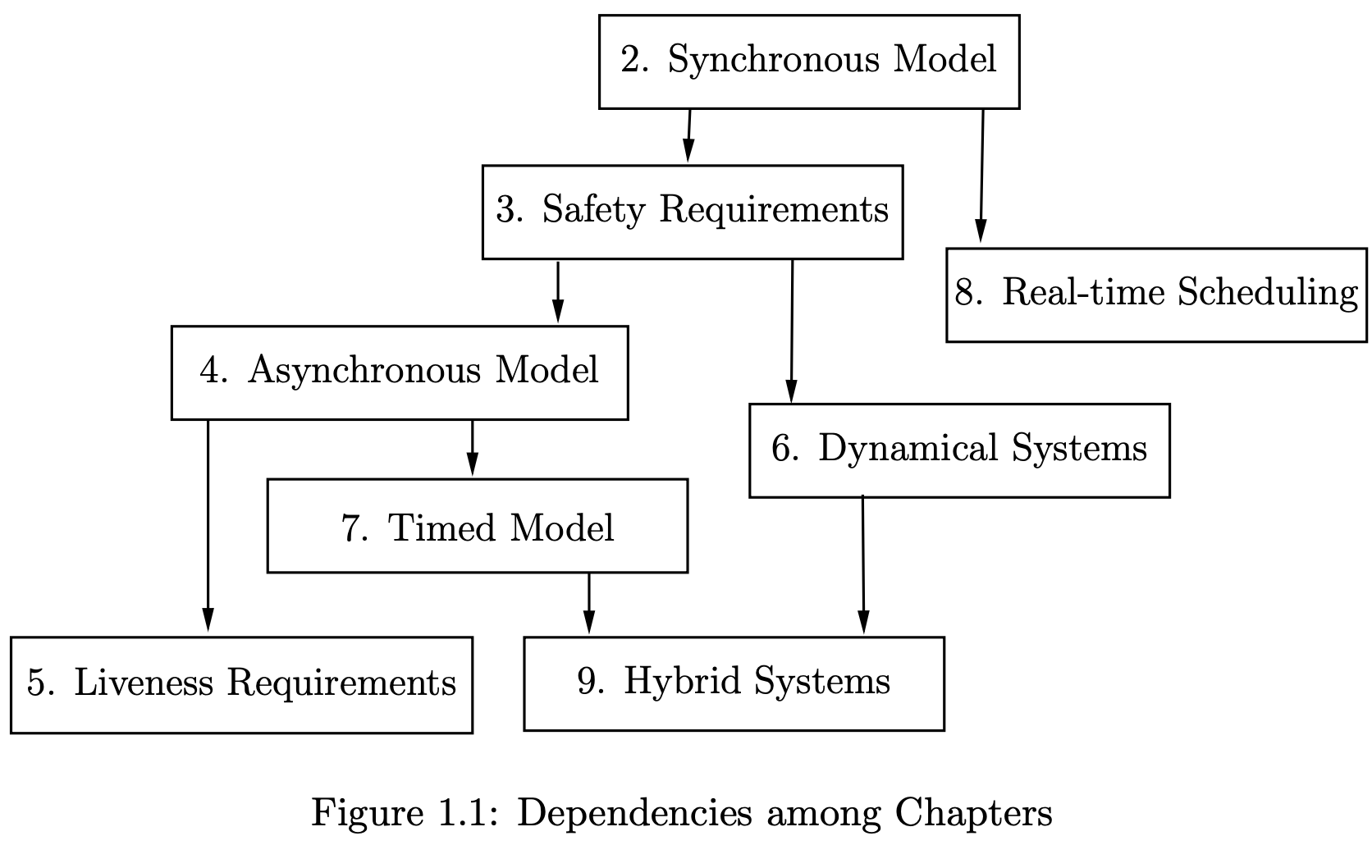
*Synchronous model (Part 1, Chapter 2)

It is a model where all the components execute in a sequence of (logical) rounds in lock-step. Within each component, code order matters for evaluating outputs and updating state. This is also known as the synchrony hypothesis, where the model assumes zero execution time for the components. So components reads input, computes output, updates internal state. Here production of output and reception of input occurs at the same time. When multiple components are composed, they all execute simultaneously and synchronously.

TLDR: The synchronous model is a discrete and synchronous model of reactive computation where all components execute in a sequence of rounds. In each round, a reactive component:

1. Reads its inputs
2. Based on current state and inputs, computes outputs
3. Updates internal state

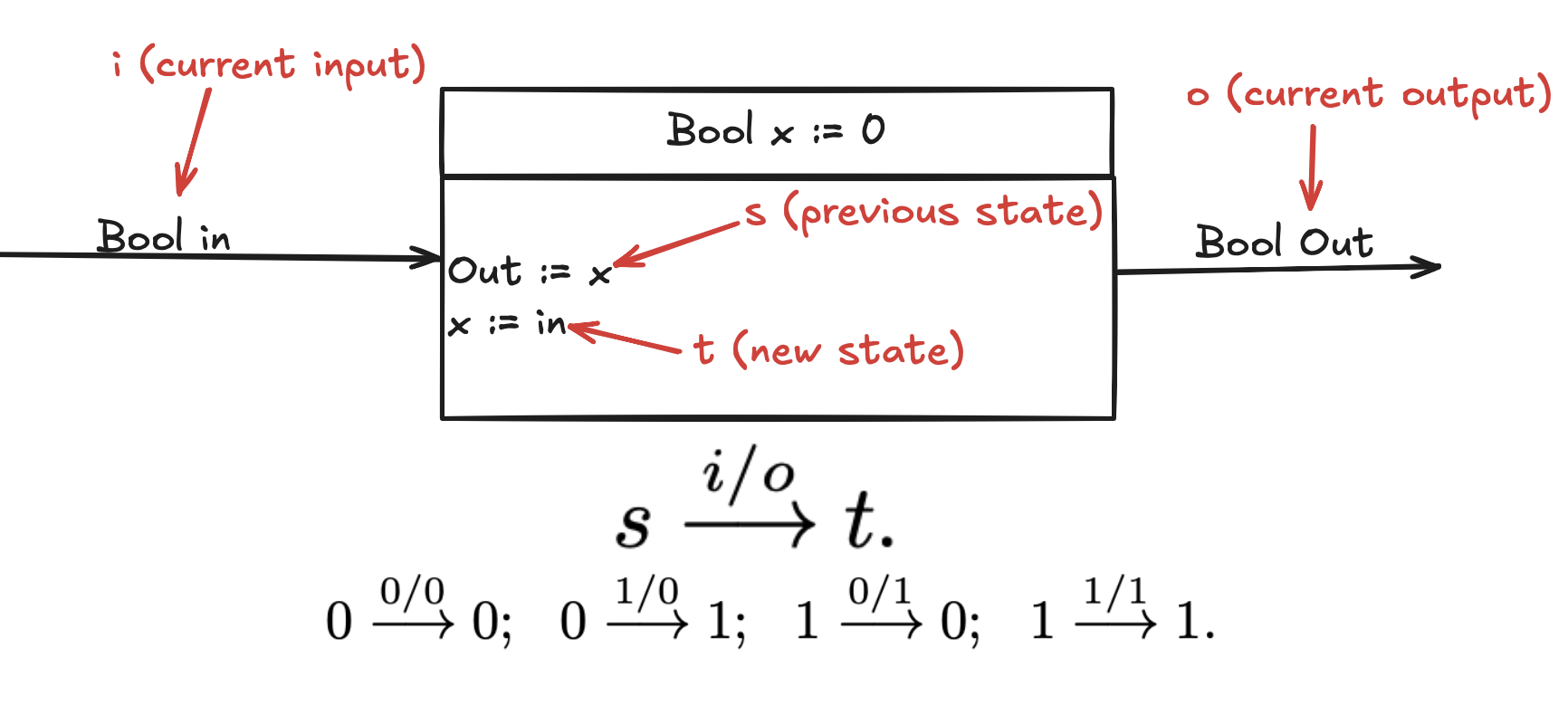
Mealie Machine example: Here is an “algorithm” for making a mealie machine:

1. Answer the following questions:

• What is the set of states?
• What are the inputs?
• What are the outputs?
• What is the initial state?

2. With the answers to these questions, you create an automaton like this:

• Each state gets a node.
• Mark the initial state.
• For each state s that can transition to a state t in one step, add an edge s → t.
• For each edge, write all possible input/output pairs corresponding to that transition.

Now let’s try it.

• There are two Boolean state variables, so the set of states is {(0,0), (0,1), (1,0), (1,1)}.
• I presume there is a single input in (not visible).
• I presume there is a single output out (not visible).
• The initial state is (0,0).

• We draw four nodes.
• Node (0,0) gets marked as initial.
• I will not go through all edges. In each state, we can have two possible inputs (0 or 1), and the component is deterministic; so there should be two transitions from each state (i.e., 8 in total). The transitions from the initial state are (0,0) —0/0⇒ (0,1) and (0,0) —1/0⇒ (1,1).

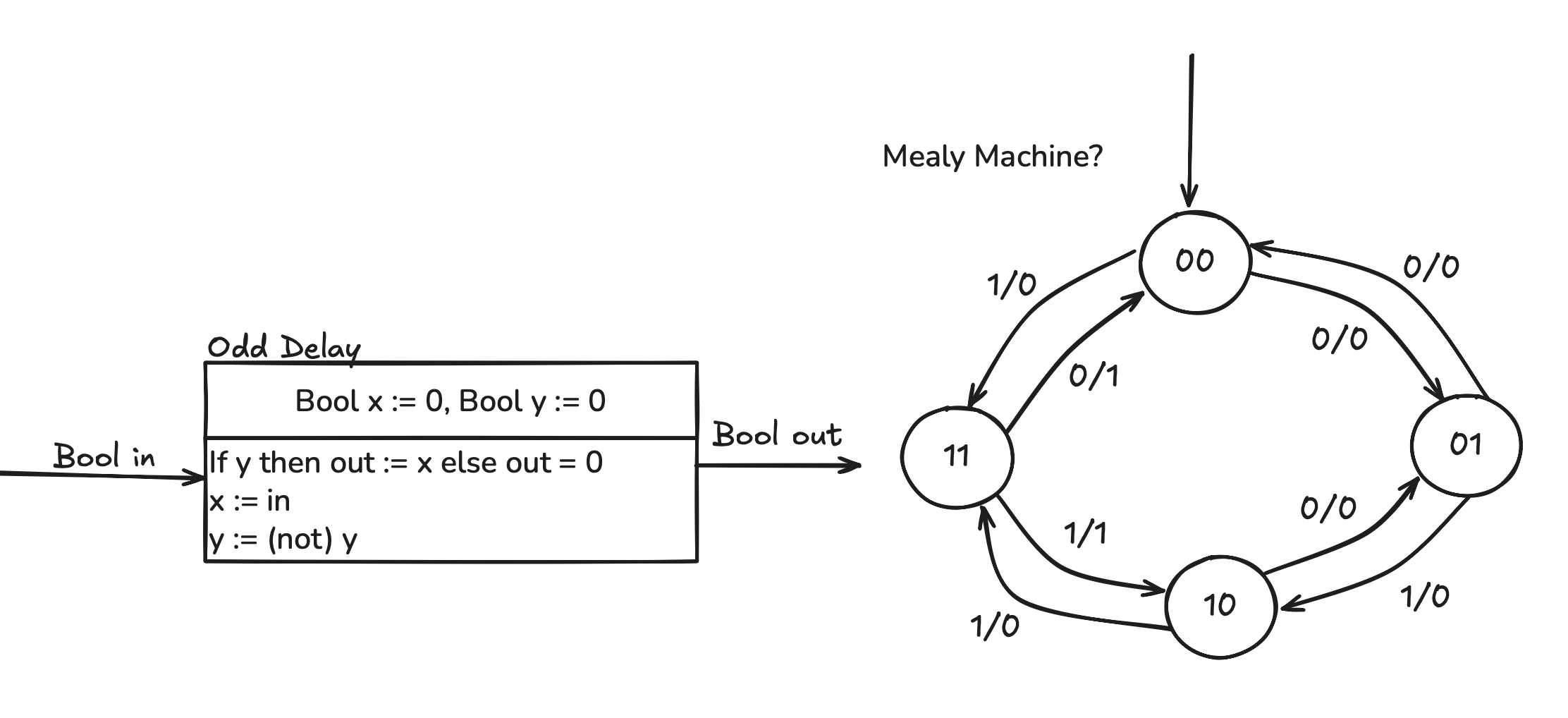
Event triggered Component

Termonology:

• A Component = The entire box seen above.
  • Initialization = Top part of a Component
  • A Reaction ( React ) = A theoretical run scenario. example( 0 — 1/0 ⇒ 1 )
  • Reaction Description = Essentially the code in the bottom box.
    • Assignment Statement = x := e
    • Conditional Statement = if b then stmt1 else stmt2
    • Auxiliary Variables = Local temporary variables that are NOT states.
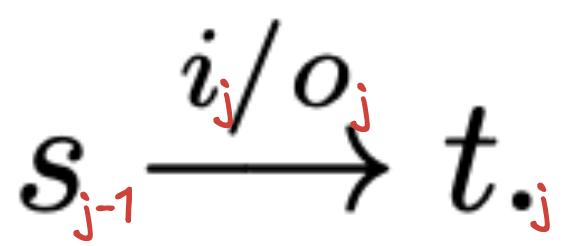
• Execution = the picture below where
• Combinational component = the picture below
• stuttering reaction = If the input is absent in a round, then the componentispassive: theoutputisabsent, andthestatestaysunchanged. Such a reaction is called a stuttering reaction.
• latched = if there exists a state variable x such that in every reaction of the component, the value of the output variable y is the updated value of the state variable.

Notes from reading

A functional component produces outputs when supplied with inputs, and its behavior can be mathematically described using a mapping between input and output values. A reactive component, in contrast, maintains an internal state and interacts with other components via inputs and outputs in an ongoing manner.

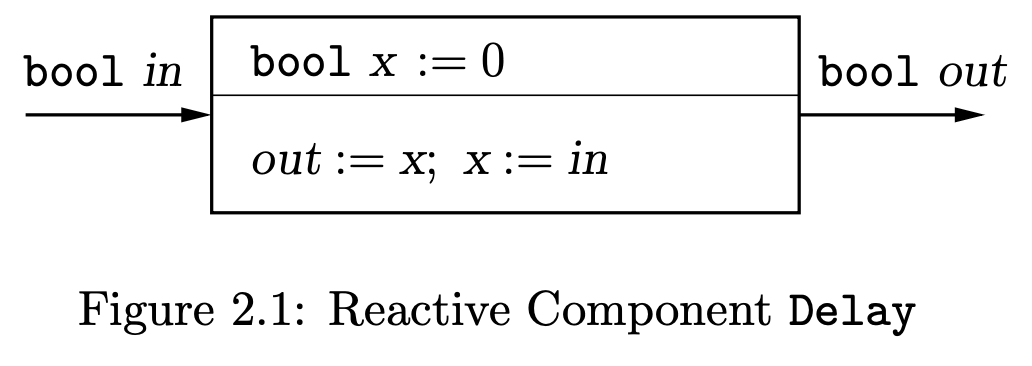This model basically returns 0 on the first run, and then on each subsiquent run it returns what the previous run put in.

Initialization

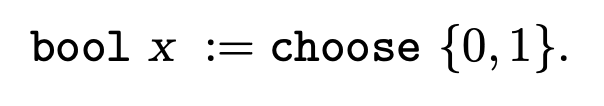In this modified version, choose may return either 0 or 1; as a result, the initial value of the variable x may be either 0 or 1. Another example of initialization using the choose construct is the declaration. 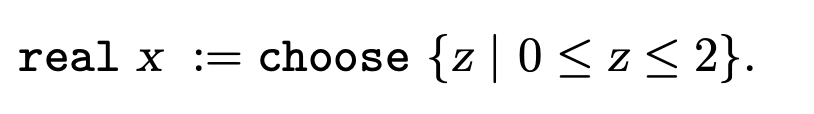This means that the variable x is real-valued, and its initial value can be any real number between 0 and 2.

Safety requirements (Part 1, Chapter 3)

Asynchronous model (Part 1, Chapter 4)

*Timed model (Part 2, Chapter 7)

• Timed processes
• Buffers with bounded delays
• Multiple clocks
• Composition
• Timed-based protocols
• Timed automata
• Zone-based symbolic analysis

We know the syntax and semantics of the timed model. We know how to model timed processes using timed automata. We know how to model timed processes in UPPAAL. We can solve mutual exclusion using a timed protocol. We can perform manually a simple zone-based symbolic analysis. Models and Tools for Cyber-Physical Systems: Timed Model

The system must also satisfy some requirements, which are formalized constraints or desired behavior the system must hold, and are used to verify the system. There are two different requirements that we look for:

Real-time scheduling (Part 2, Chapter 8)

*Continuous model (Part 3, Chapter 6)

A continuous-time component is similar to the execution of a deterministic synchronous reactive component, except the notion of a round is now infinitesimal: at every time t, the outputs at time t are determined as a function of the inputs at time t and the state of the component at time t, and then the state is updated using the rate of change specified by the derivative evaluated using the inputs and state at time t.

For example, a safety requirement for a cruise controller can demand that the speed of the car should always be below some maximum speed, and a liveness requirement can demand that the difference between the actual speed and the desired speed should eventually be close to zero. A cruise controller, however, has a new kind of requirement, namely, that small perturbations in input values, such as the grade of the road, should not cause disproportionately large changes in the speed of the car. This requirement, which is relevant only for continuous-time systems, is called stability.

• Explain the P, I and D in PID  PID = a proportional term capturing the reaction to the current error, an integral term capturing the reaction to the cumulative error, and a derivative term capturing the response to the rate of change of error

• Proportional (P): Reacts to the current error (difference between desired and actual value). Example: If you want 60 km/h but you’re at 50 km/h, the error is 10 km/h, so P applies a correction proportional to that (e.g., accelerate harder if the error is bigger). This is spot-on in your description.

• Integral (I): Reacts to the cumulative (or accumulated) error over time. It sums up past errors to eliminate “steady-state” issues where the system settles at a value slightly off the target (e.g., if wind resistance keeps you at 58 km/h instead of 60, I gradually ramps up the correction to push you exactly to 60). Think of it as fixing long-term drift or bias—it’s like noticing you’ve been a bit slow for a while and adding extra throttle to catch up.

• Derivative (D): Reacts to the rate of change of the error (how fast the error is increasing or decreasing). It helps reduce overshoot (e.g., preventing you from blasting past 60 km/h to 70) and smooths the output graph by damping rapid changes, making the response more stable. Your description is close but has typos: it’s “overshoot” (not overshot), “smooths” (not smothes), and “output” (not outout).

• What is the interplay between stability and control?

  • Trade-offs: Control gains (e.g., in PID terms) must balance responsiveness (quick error correction) with stability—high gains might cause overshoot or instability, while low gains ensure stability but slow response.

• Explain the Euler algorithm; What is the different to Runge-Kutta algorithm? Euler’s method estimates the state at the end of an interval by assuming that the rate of change of state stays constant during the interval, and this rate is based only on the state at the beginning of the interval. A better approximation can be obtained if the estimated change in the state at the end of the interval is used to estimate a change in the derivative, and this is used to readjust the state estimate. Runge-Kutta methods comprise a popular class of numerical integration methods based on this idea.

• Derive the a P/I/D-controller for this (-given by us to you-) continuous model; start by identifying the outputs, the controls, the state equations …

• Explain the concept of stability on an example (perhaps the example will be given by us; or you pick it yourself and we modify it during the discussion)

• Give an example of a linear system; argue why it is linear

Hybrid model (Part 3, Chapter 9)