security Guy uses vim and blue slides
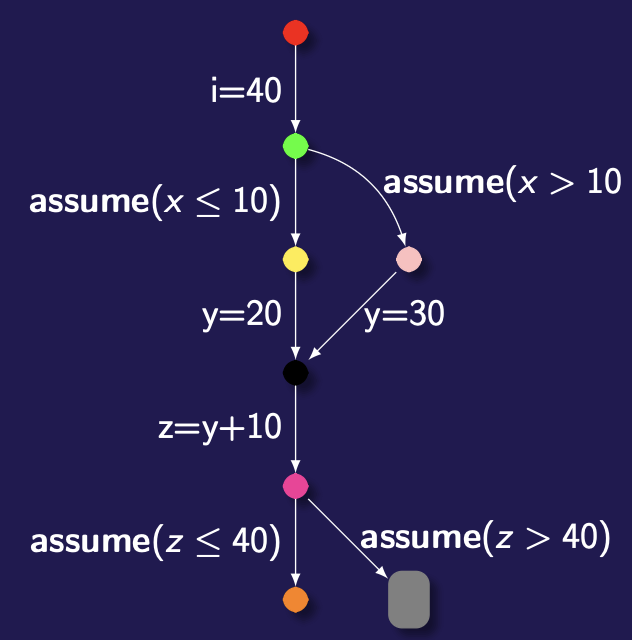
i = 40
assume(x ⇐ 10) → y = 20 or assume(x > 10) → y = 30
z = y + 10
assume(z ⇐ 40) → orange or assume(z>40) → grey

States S = L X
States S = L × VStates × MStates Transfer Function Trans : S × E → 2
/* Initial assignment */ Trans(⟨l₀, V, M⟩, (l₀, i = 40, l₁)) = {⟨l₁, V[i ↦ 40], M⟩}
/* Branching on x */ Trans(⟨l₁, V, M⟩, (l₁, assume(x ≤ 10), l₃)) = { ⟨l₃, V, M⟩ if (EB8(V, M)(x ≤ 10) \ {0}) ≠ ∅ ∅ otherwise }
Trans(⟨l₁, V, M⟩, (l₁, assume(x > 10), l₄)) = { ⟨l₄, V, M⟩ if (EB8(V, M)(x > 10) \ {0}) ≠ ∅ ∅ otherwise }
/* Assignments to y based on branch */ Trans(⟨l₃, V, M⟩, (l₃, y = 20, l₅)) = {⟨l₅, V[y ↦ 20], M⟩}
Trans(⟨l₄, V, M⟩, (l₄, y = 30, l₅)) = {⟨l₅, V[y ↦ 30], M⟩}
/* Calculating z */ Trans(⟨l₅, V, M⟩, (l₅, z = y + 10, l₆)) = {⟨l₆, V[z ↦ i], M⟩ | i ∈ EB8(V, M)(y + 10)}
/* Determining final state */ Trans(⟨l₆, V, M⟩, (l₆, assume(z ≤ 40), l₇)) = { ⟨l₇, V, M⟩ if (EB8(V, M)(z ≤ 40) \ {0}) ≠ ∅ ∅ otherwise }
Trans(⟨l₆, V, M⟩, (l₆, assume(z > 40), l₈)) = { ⟨l₈, V, M⟩ if (EB8(V, M)(z > 40) \ {0}) ≠ ∅ ∅ otherwise }
lll