Decidable?

Key Concepts for Exam question:

1. Decidable: A language has an algorithm that always halts and answers “yes” or “no”.
2. Recognizable (RE): A language has an algorithm that halts on “yes” instances (may loop on “no”).
3. $P$: Problems solvable in polynomial time.
4. $NP$: Problems verifiable in polynomial time (or solvable with a polynomial-time “lucky guess”).
5. $NP$-hard: Problems at least as hard as all problems in $NP$ (if $NP\ne P$, these aren’t in $P$).

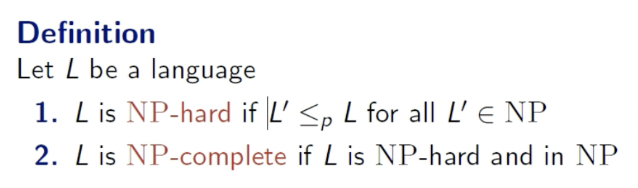
np is hard if lprime is in np.

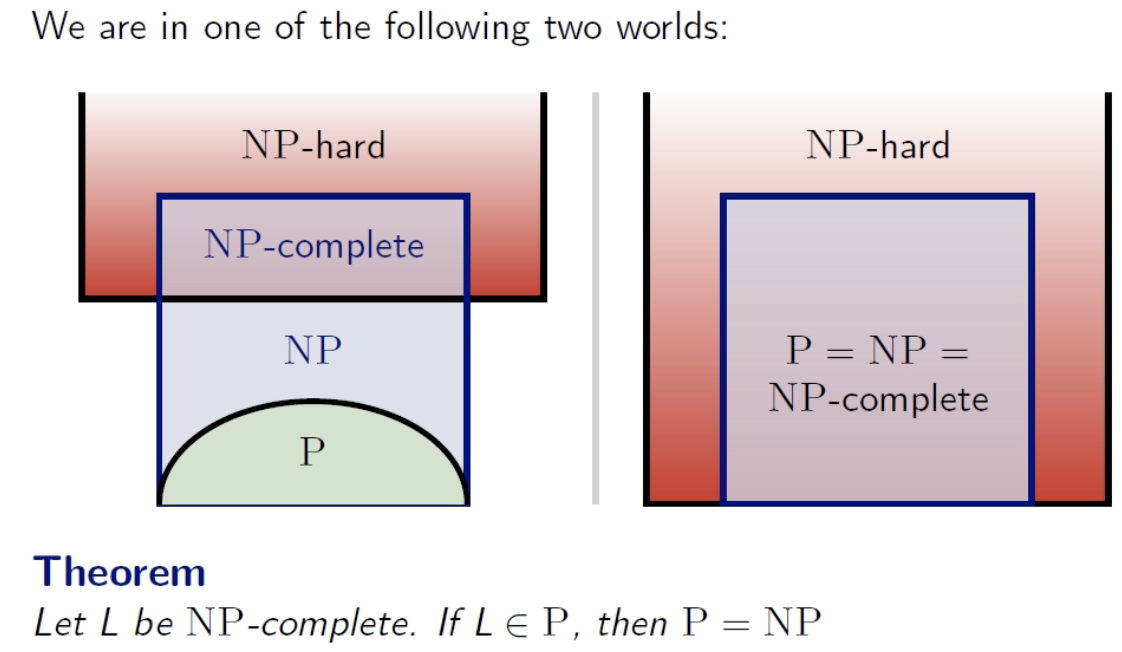
Key Relationships:

• Reductions:
  • If $A{\le }_{p}B$:
    • $B\in NP$ ⇒ $A\in NP$
    • $A$ is $NP$-hard ⇒ $B$ is $NP$-hard
• Hierarchy:
  • $P\subseteq NP\subseteq$ Decidable $\subseteq$ Recognizable
• $NP$-hard + $NP$ ⇒ $NP$-complete.

---

Language Analysis:

$L_1$

Given:

• $SAT{\le }_p{L}_1$ (SAT reduces to $L_1$)
• $L_1$ is $NP$-hard, not in $P$
• Unknown: Decidability, $NP$ membership

Conclusions:

1. Decidable? ❓
   • $NP$-hardness ≠ decidability (undecidable problems can be $NP$-hard).
2. Recognizable? ❓
   • Recognizability depends on decidability.
3. $NP$? ❓
   • $NP$-hardness ≠ $NP$ membership (unless $NP=co\text{-}NP$).
4. In $P$? ❌
   • $NP$-hard + $P\ne NP$ ⇒ $L_1\notin P$.

---

$L_2$

Given:

• $L_2{\le }_{p}SAT$
• Known: Decidable, in $NP$
• Unknown: $NP$-hardness, $P$ membership

Conclusions:

1. Decidable? ✅
   • All $NP$ languages are decidable.
2. Recognizable? ✅
   • Decidable ⇒ Recognizable.
3. $NP$? ✅
   • $L_2{\le }_{p}SAT$ ($SAT\in NP$) ⇒ $L_2\in NP$.
4. $NP$-hard? ❓
   • Reduction direction: $L_2{\le }_{p}SAT$ ⇒ $L_2$ isn’t necessarily $NP$-hard.

---

$L_3$

Given:

• Two deciders ($M_1$: $O(n^2)$, $M_2$: $O(2^n)$)
• Known: Decidable, in $P$

Conclusions:

1. Decidable? ✅
   • Explicitly stated.
2. Recognizable? ✅
   • Decidable ⇒ Recognizable.
3. $NP$? ✅
   • $P\subseteq NP$ ⇒ $L_3\in NP$.
4. $NP$-hard? ❌
   • If $L_3\in P$ and $P\ne NP$ ⇒ $L_3$ isn’t $NP$-hard.

---