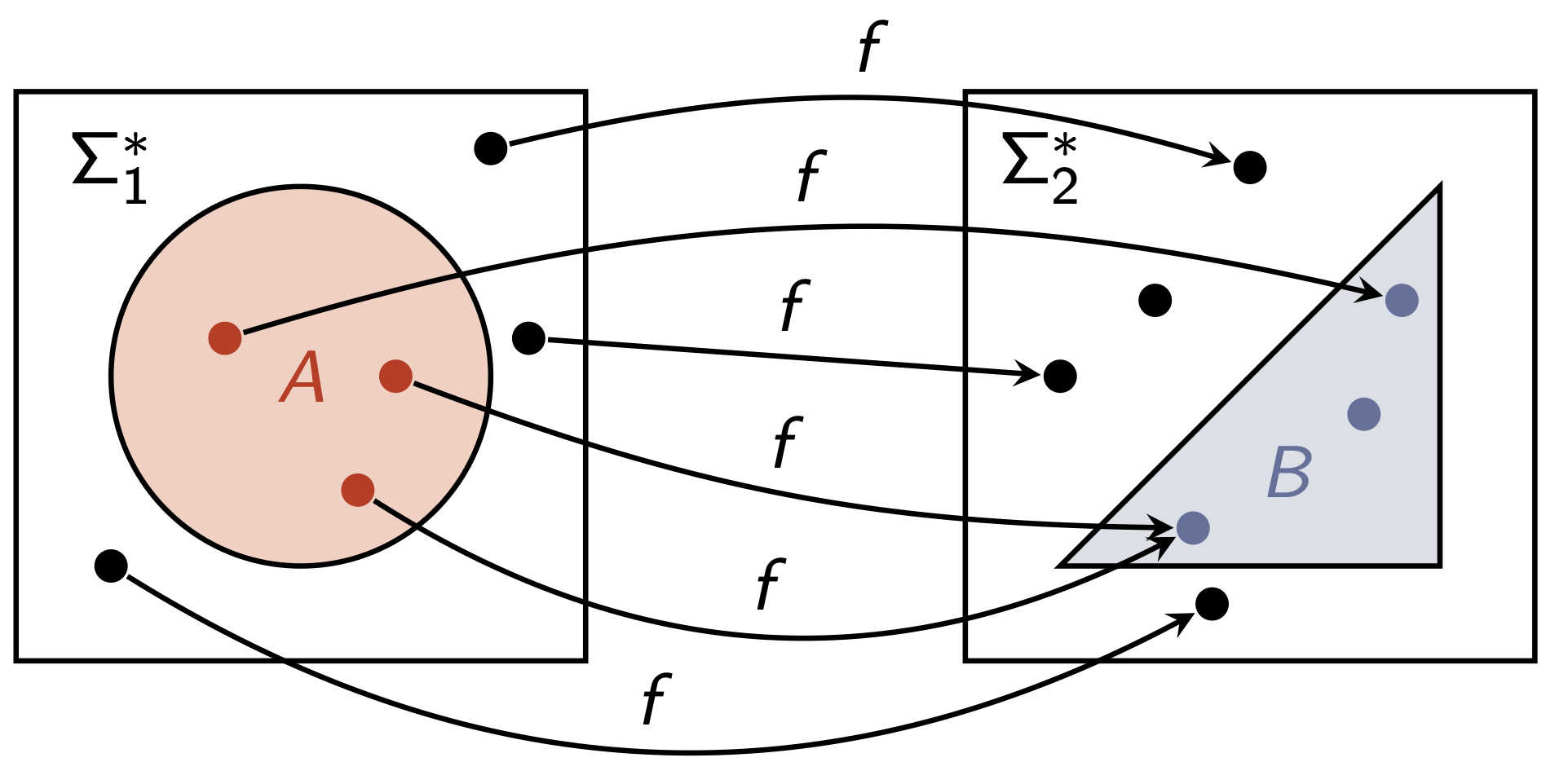
A ≤ B (A reduces to B)
- B is at least as hard as A
- A is at most as hard as B
When A is decidable/easy:
decidable ≤ B (decidable language reduces to B)
- B is at least as hard as decidable languages
- B can be: decidable OR undecidable OR not recursively enumerable
- We cannot determine B’s computability class from this information alone
When B is decidable/easy:
A ≤ decidable (A reduces to decidable languages)
- A is at most as hard as decidable languages
- A must be decidable
- This gives us strong information about A
When A is hard (like HP):
HP ≤ B (HP reduces to B)
- B is at least as hard as HP
- B must be undecidable (cannot be decidable)
When B is hard (like HP):
A ≤ HP (A reduces to HP)
- A is at most as hard as HP
- A can be: decidable OR undecidable (but still recursively enumerable)
- A cannot be: harder than HP (i.e., not recursively enumerable)
- We cannot determine A’s exact computability class
Key Principle
The “easy target” gives us information, the “hard source” gives us information:
- If something easy can solve the target → target is easy
- If the source is hard → target must be hard
- If something reduces to something hard → we learn nothing about the source
- If something easy reduces to the target → we learn nothing about the target
This explains why your results show “we don’t know” in cases where you’re reducing from something easy or to something hard.

If still confused look at selfstudy 3 and Decidable?