selfstudy 3

1) No it is the other way around, because b has stuff a doesnt have, but a ONLY has things b already has.

No because B will have some things a doesnt, so maybe it doesnt work. Look at the picture below ()

True because if a doesnt work then b WILL not work because they share those exact components. Look at the picture below.

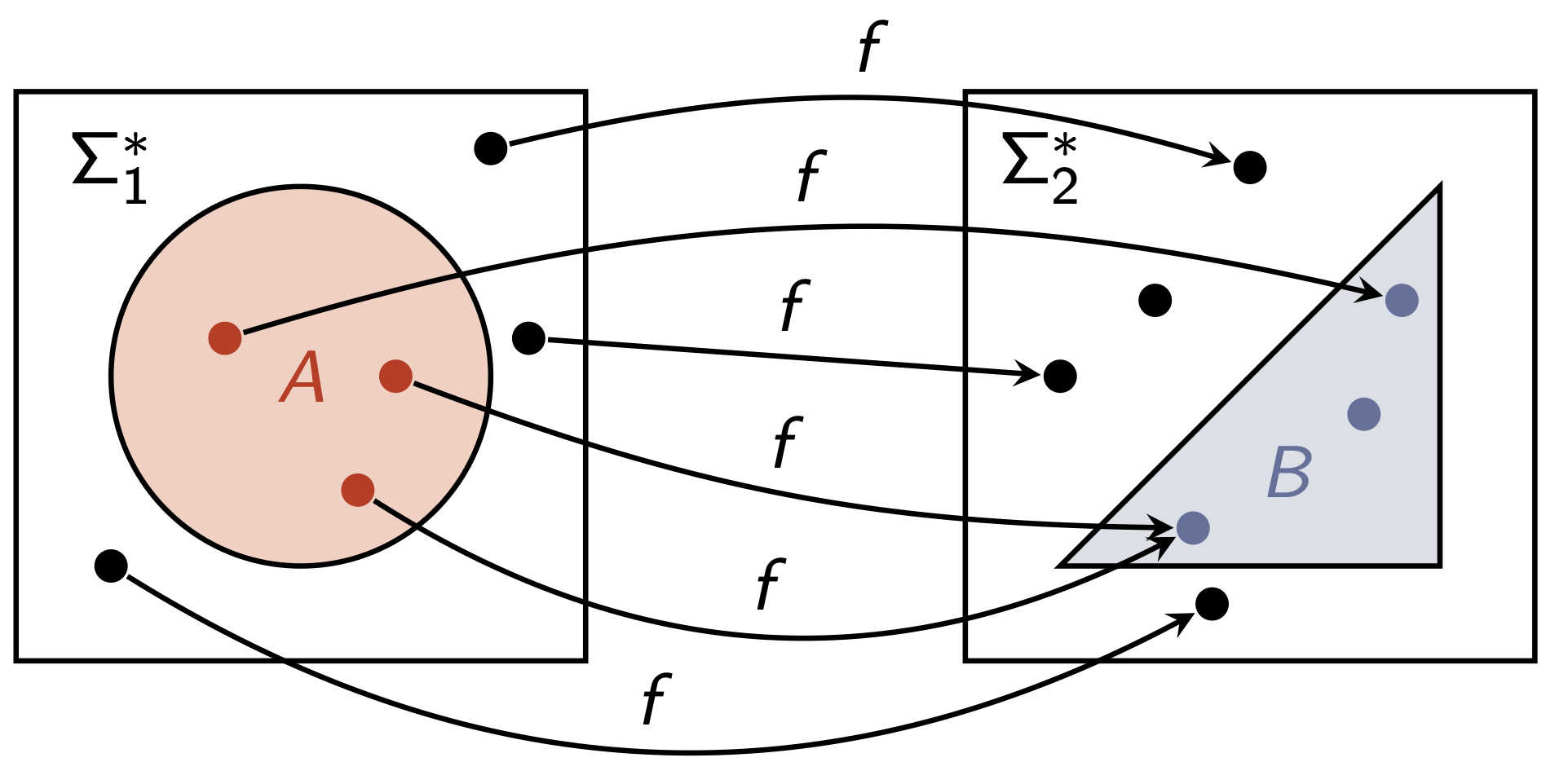
Essentially the larger the language is the higher chance it has to be computable.

Reduction Relationships and Computability

task2

$\forall w\in L_1,f(w)=w$

1. true
2. false because we just found that L1 is true. And complements means that it is the opposite (idk)
3. false because if it at most accepts one word it CAN accept 0 which isnt computably enumerable, and becasue there arent an infinite amount of solutions
4. true since the previous one is NOT then the compliment must be true because it is the same as language L1.
5. false

Flawed argument: It is tempting to say that L5 = L1 ∩ L3, and so we would need to solve L1 and

L3, but L3 is not computably-enumerable. But such an argument is generally flawed (why?). Argument: We cannot come up with an enumeration algorithm, since we would not know when to accept. We can search for the first word that is accepted, but then there may always exist another word that is also accepted; hence, we can never terminate the search.

6. False Because if the other language accepts only 1 then the compliment could accept zero, which is bad.

Identity function is essentially just a linear graph that hits (1,1) (2,2) (3,3) and so on. And it is computable.

1. The solution is a fancy way of saying that every number is indeed itself. so yes 1 does indeed equal to 1.

2. the solution is just a stupidly fancy way of saying that if l1 is smaller or equals to l2 which itself is smaller than or equals to l3, then l1 is indeed smaller than or equals to l3

Essentially we need to show that for every word in even it is even, but if you do a +1 then it is odd. every word NOT in even is odd, and when you +1 it is even. (also if you have nothing it is nothing, so nothing isnt in the set)

$$U=\{┌M┐|L(M)=\{0,1\}\ast \}$$

It is essentially just regex for a language that accepts everything. (you can mostly ignore the first half)