Exercise 1


⊥, 21 → ⊤, 2.

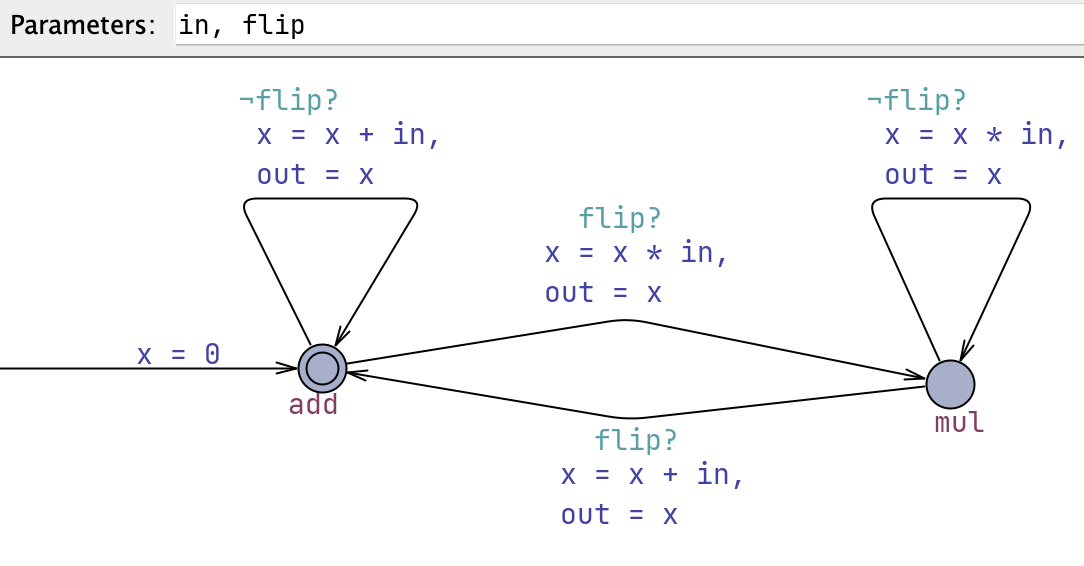
Exercise 2
 A)
Because they arent even in the initial state. he made a mistake in Session 3 Safety requirements (part 1) part 3 because he forgot about the initial state.
A)
Because they arent even in the initial state. he made a mistake in Session 3 Safety requirements (part 1) part 3 because he forgot about the initial state.
B) Either x and y are the same, or x is twice as large as y.
C)
(x = y ∧ z = 1) ∨ (x = 2y ∧ z = 0)
Exercise 3
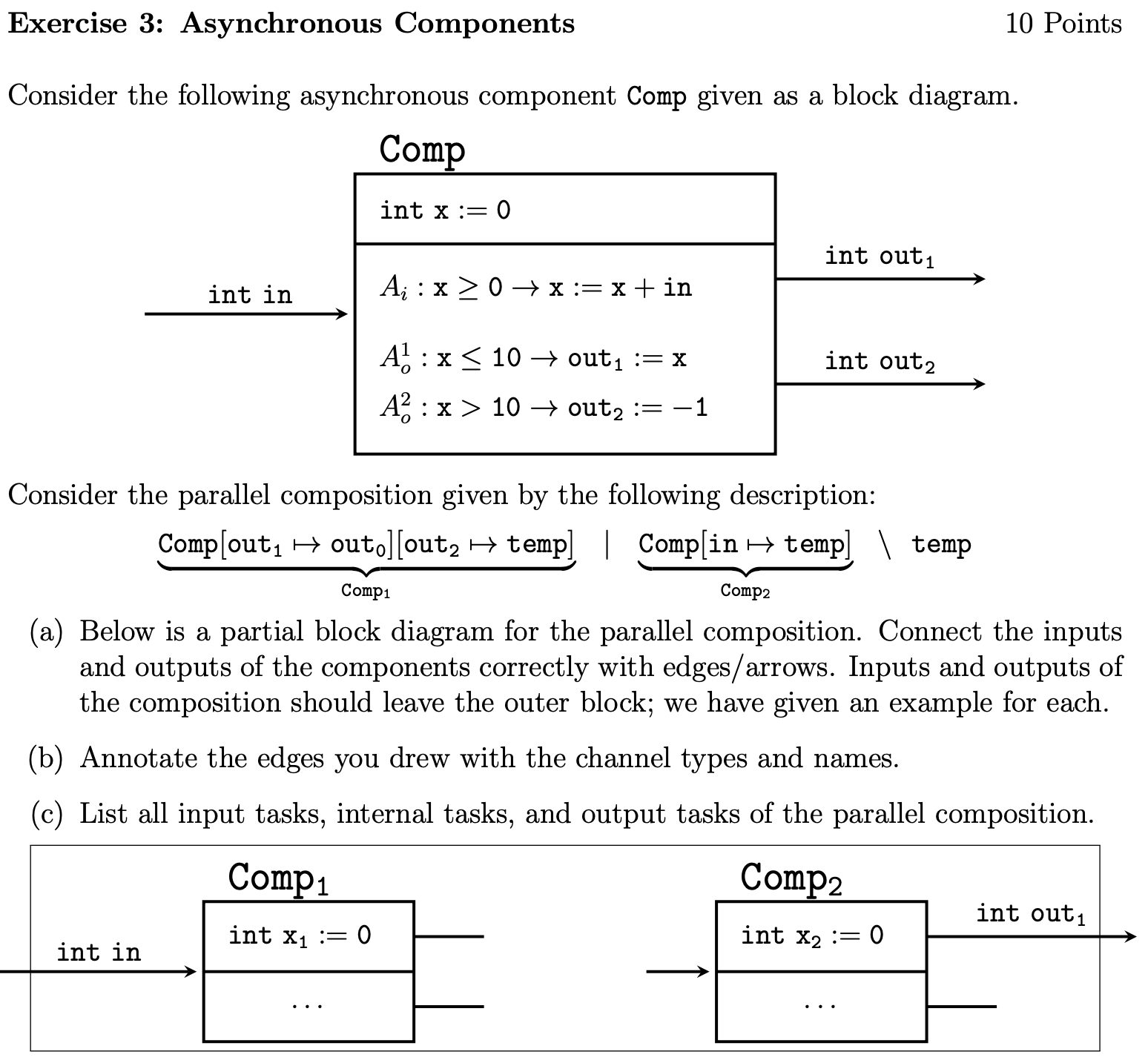
A) and B)
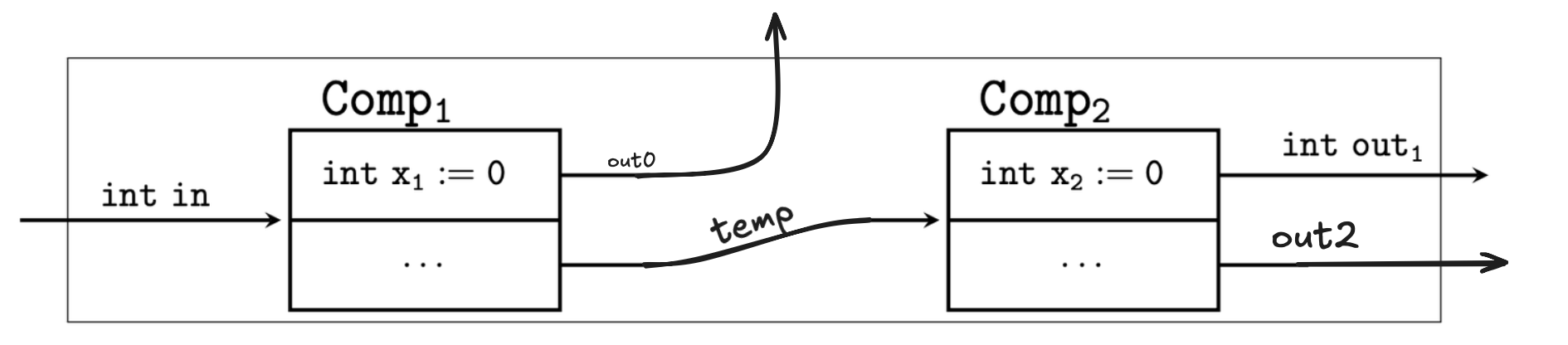
C)
Input:
- Ai: x1 >= 0 ⇒ x1 := x1 + in
Internal:
- At: x1 > 10 ∧ x2 ≥ 0 → {temp := −1; x2 := x2 + temp}
Output:
- A1o: x1 ≤ 10 → out0 := x1
- A2o: x2 ≤ 10 → out1 := x2
- A3o: x2 > 10 → out2 := −1
Exercise 4
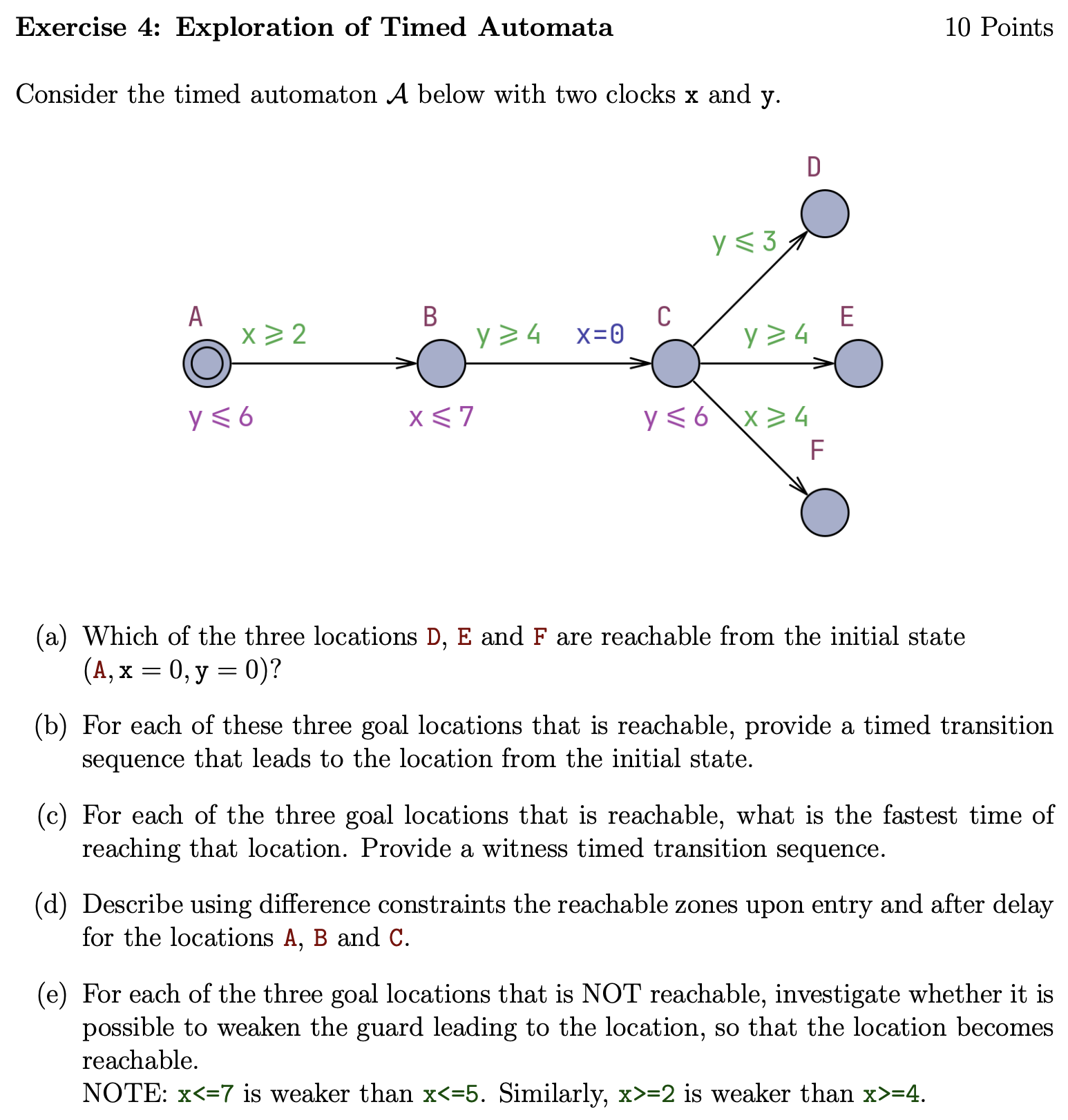
a) Only E is reachable because in D y needs to be 3 but it is at least 4, and in F for x to reach 4 y would need to be 8, but the invariant says we need to leave on or before y reaches 6.
b) (A, x = 0, y = 0) 2 → (A, x = 2, y = 2) → (B, x = 2, y = 2) 2 → (B, x = 4, y = 4) −→ (C, x = 0, y = 4) −→ (E, x = 0, y = 4)
c) 4.
d)
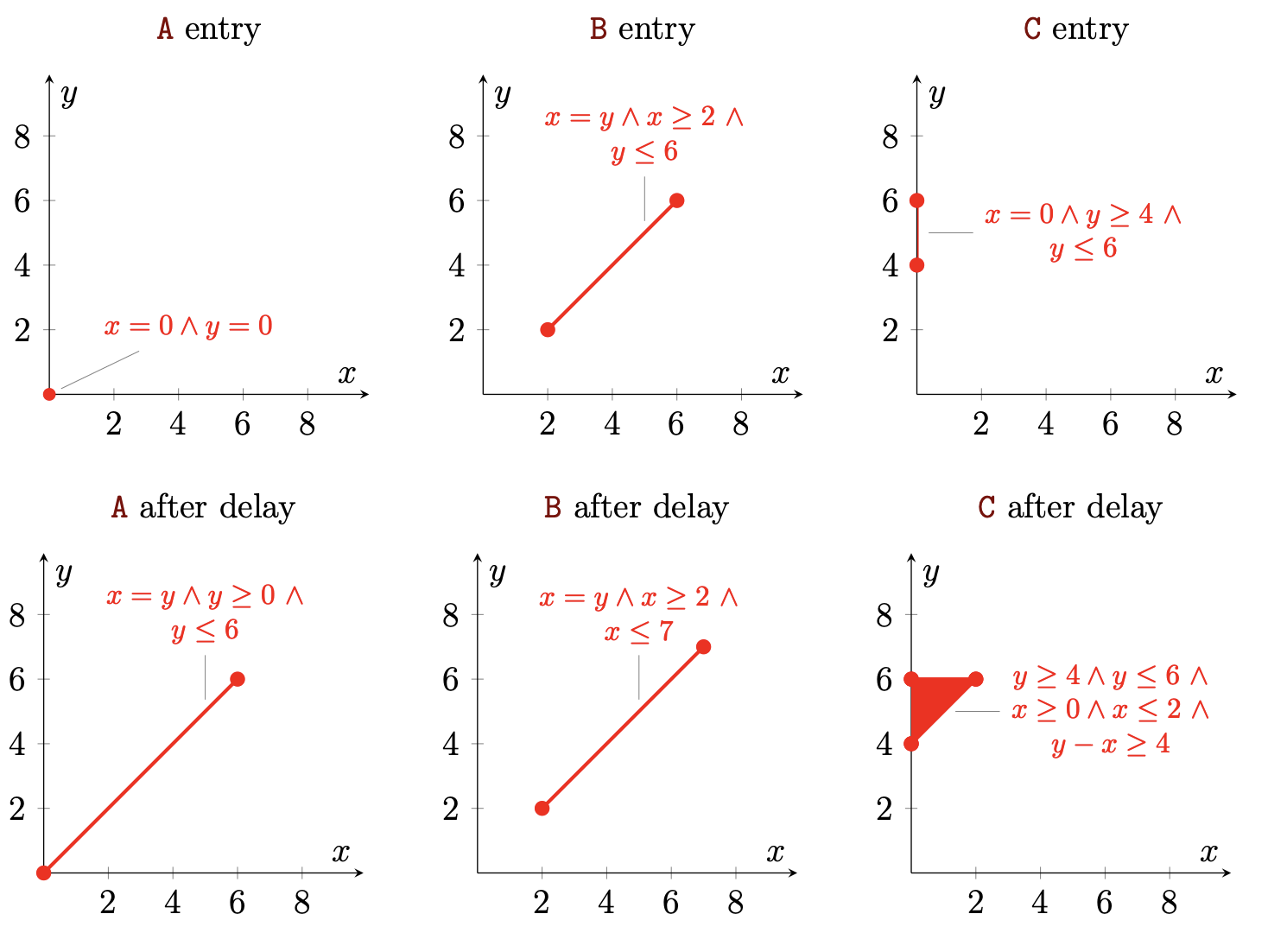
e)
Changing the guard to y ≤ 4 will make D reachable. Changing the guard to x ≥ 2 will make F reachable.
Exercise 5
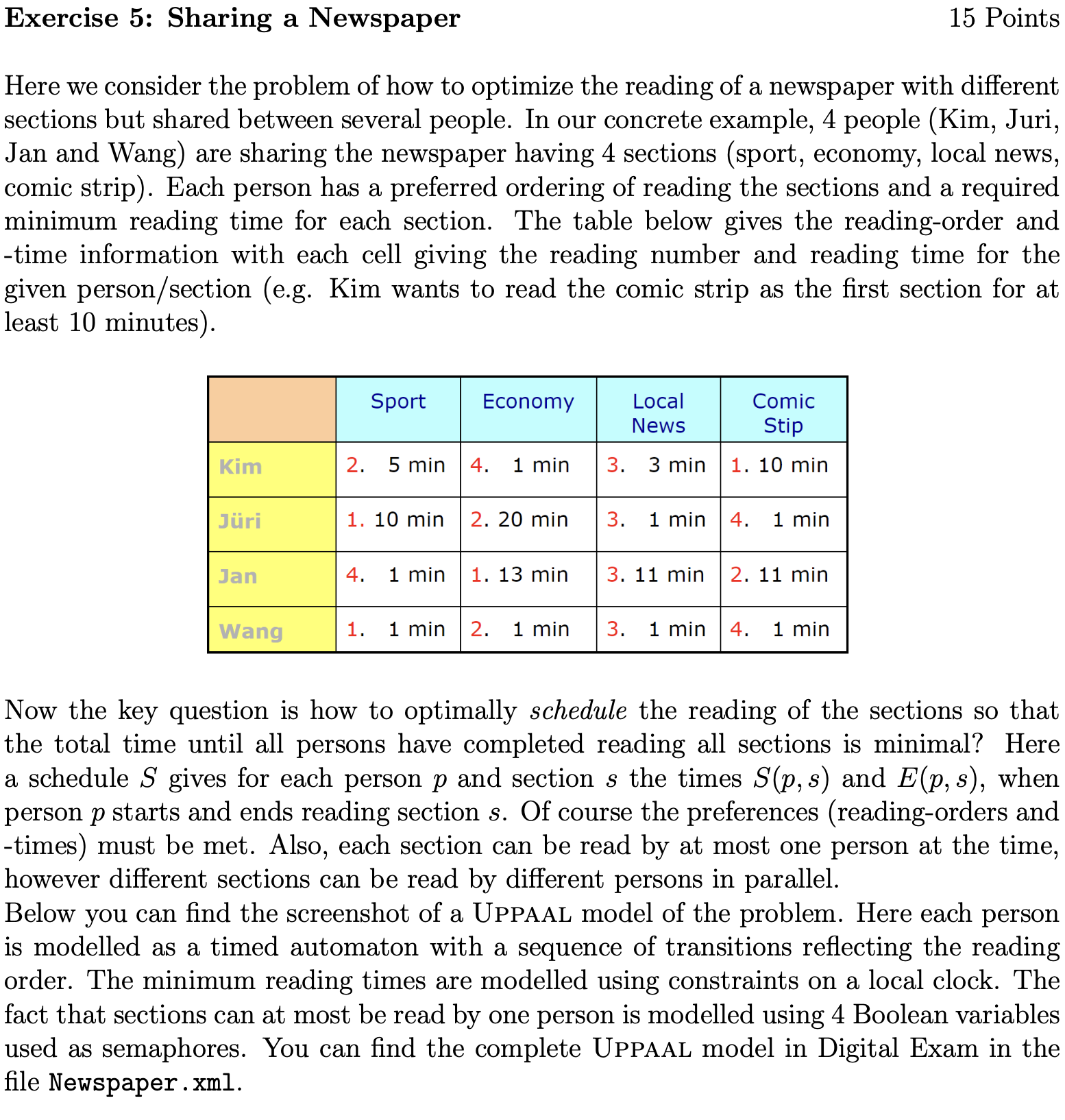
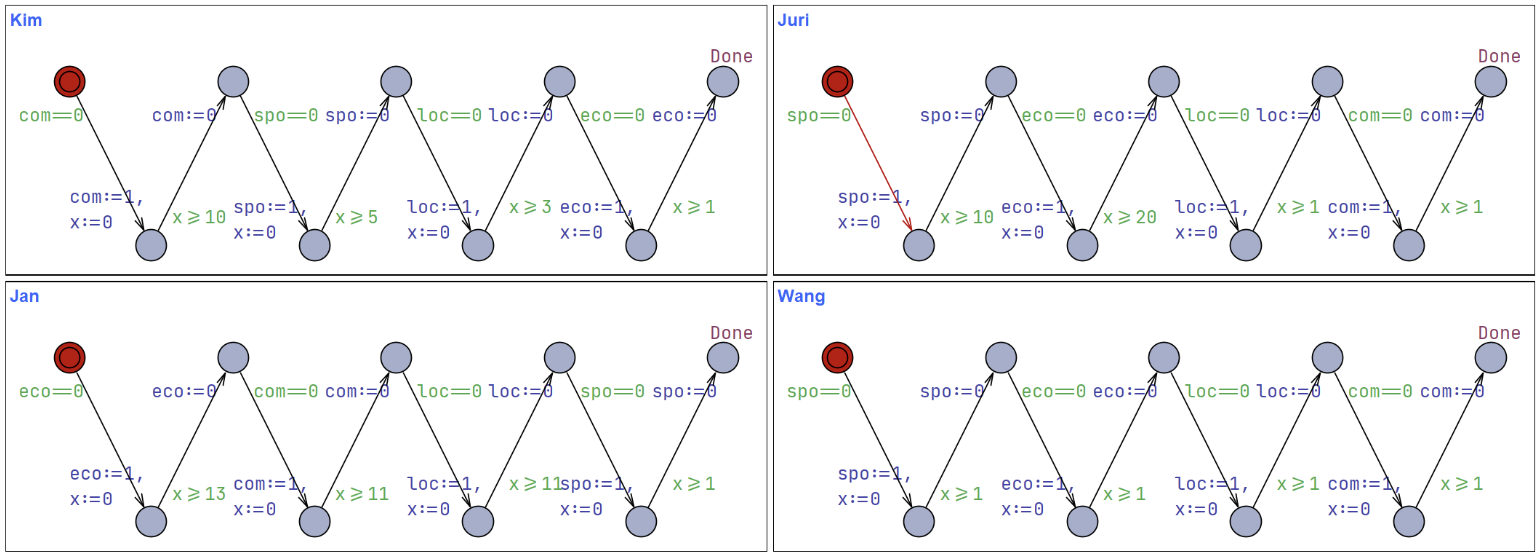
#!/bin/python3
import matplotlib.pyplot as plt
def f(x, t):
# Implements the simplified quadcopter model
m = 0.5
g = 9.81
kp = 10
r = 0.0
der_v = -g + (1/m)*x[0]
# You should return an array of state derivatives
return [...]
def main():
x0 = [0, 0] # Initial state
t0 = 0 # Initial time
T = 10 # Time horizon
fig, ax = plt.subplots()
experiment(x0, t0, 0.01, T, ax)
ax.set_xlabel("t")
ax.legend()
plt.show()
# -------------------------------------------------------
# Code below does not need to be changed during the exam.
def runge_kutta_4(f, x0, t0, h, N):
t = [t0]
result = [x0]
for i in range(N):
xi = result[-1]
k1 = f(xi, t[-1])
k2 = f(extend(xi, h/2, k1), t[-1] + h/2)
k3 = f(extend(xi, h/2, k2), t[-1] + h/2)
k4 = f(extend(xi, h, k3), t[-1] + h)
step = []
for j in range(len(xi)):
step.append(xi[j] + h/6 * (k1[j] + 2*k2[j] + 2*k3[j] + k4[j]))
result.append(step)
t.append(t[-1] + h)
return t, result
def extend(x, h, der):
assert(len(x)) == len(der)
result = []
for j in range(len(x)):
result.append(x[j] + h * der[j])
return result
def convert(data):
result = []
for i in range(len(data[0])):
result.append([])
for x in data:
for i in range(len(x)):
result[i].append(x[i])
return result
def experiment(x0, t0, h, T, ax):
N = round(T / h)
t, result = runge_kutta_4(f, x0, t0, h, N)
result = convert(result)
for i in range(len(result)):
if i == 0: # Only plot state 0, which is the height.
ax.plot(t, result[i], label=f's[{i}](t)')
if __name__ == '__main__':
main()