- We define safety and liveness properties.
- We define transition systems and reachable states.
- We define invariants as an important class of safety properties.
- We show how to prove that a property is an invariant of a system using inductive invariants.
Syntax cheatsheet can be found here Temporal Logic and Set-Builder Notation Reference
a) {s0 → s1 → s2 → · · · | ∀i : si |= a ∨ b} This is an invariant and therefore a safety property (but not a liveness property). because it states “something bad never happens”, and the properties hold at every state in every execution. But it does not say “something good eventually happens”.
b) {s0 → s1 → s2 → · · · | ∀i : si |= ¬b U a} This one is says “something bad never happens”, so it has the Safety property.
c) {s₀ → s₁ → s₂ → ··· | ∀i : sᵢ |= a → ∃j > i : sⱼ |= b} Liveness property because “something good eventually happens”
d) {s0 → s1 → s2 → · · · | |{i | si |= a}| = 3} This is neither a safety property (and hence not an invariant) nor a liveness property. We saw that every property can be described as the intersection of a safety property and a liveness property. Here, the property is the intersection of “3 or fewer states satisfy a” and “3 or more states satisfy a.” The former is a safety property and the latter is a liveness property.
e) {s0 → s1 → s2 → · · · | (∀i ∃j > i : sj |= a) → (∀i ∃j > i : sj |= b)} “IF a occurs infinitely often, THEN b must also occur infinitely often”
f)
{s₀ → s₁ → s₂ → ··· | ∃i ∀j > i : ¬(sⱼ |= a)} This defines: “The set of all infinite state sequences where there exists some point after which property a never occurs again”
This is a liveness property (and not a safety property and hence not an invariant).
Exercise 2
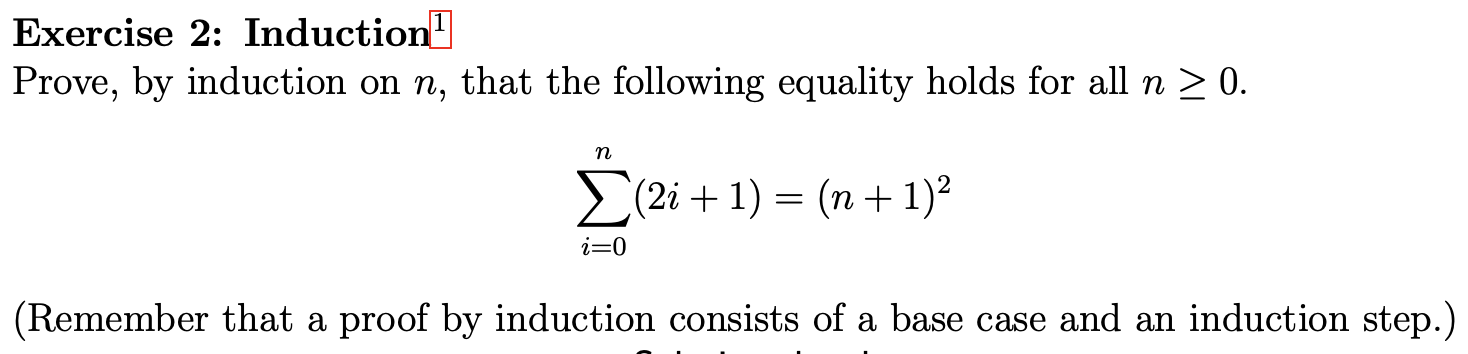
Exercise 3
a) No because the property hold at every state in every execution except for the first one, where 0 cannot be 0 + 1. For some reason this is the case even though it breaks every second state.
b)
The formula is not an inductive invariant. As a counterexample, the state (1, 0, 0) satisfies
φ and has a transition to the state (2, 0, 1), which does not satisfy φ.
=c)= if (z 0 and x y) or (z 1 and x y + 1):