Basic Set-Builder Notation for State Sequences
Structure
{s₀ → s₁ → s₂ → ··· | condition}
Components
{…} - The outer braces indicate this is a set
s₀ → s₁ → s₂ → ··· - This represents an infinite sequence of states, where:
- s₀, s₁, s₂, etc. are individual states
- The arrows (→) indicate transitions or progression from one state to the next
- The ellipsis (···) indicates the sequence continues infinitely
| - This vertical bar means “such that” (standard set-builder notation)
Logical Operators and Quantifiers
Quantifiers
- ∀i - Universal quantifier meaning “for all i” or “for every i”
- ∃i - Existential quantifier meaning “there exists some i”
Logical Operators
- ∧ - Logical conjunction (AND)
- ∨ - Logical disjunction (OR)
- ¬ - Logical negation (NOT)
- → - Logical implication (IF…THEN)
Satisfaction Relations
- sᵢ ⊨ a - “state sᵢ satisfies property a” (models/satisfies)
- sᵢ ⊭ a - “state sᵢ does not satisfy property a” (does not model)
Temporal Logic Operators
- ¬b U a - “not b until a” (Until operator)
- Property b does not hold at any state until property a becomes true
- Once a occurs, b may or may not occur afterward
Property Classifications
Safety Properties
Properties that state “something bad never happens” - can be violated in finite time
Liveness Properties
Properties that state “something good eventually happens” - require infinite time to verify
Invariants
Properties that hold at every state in every execution.
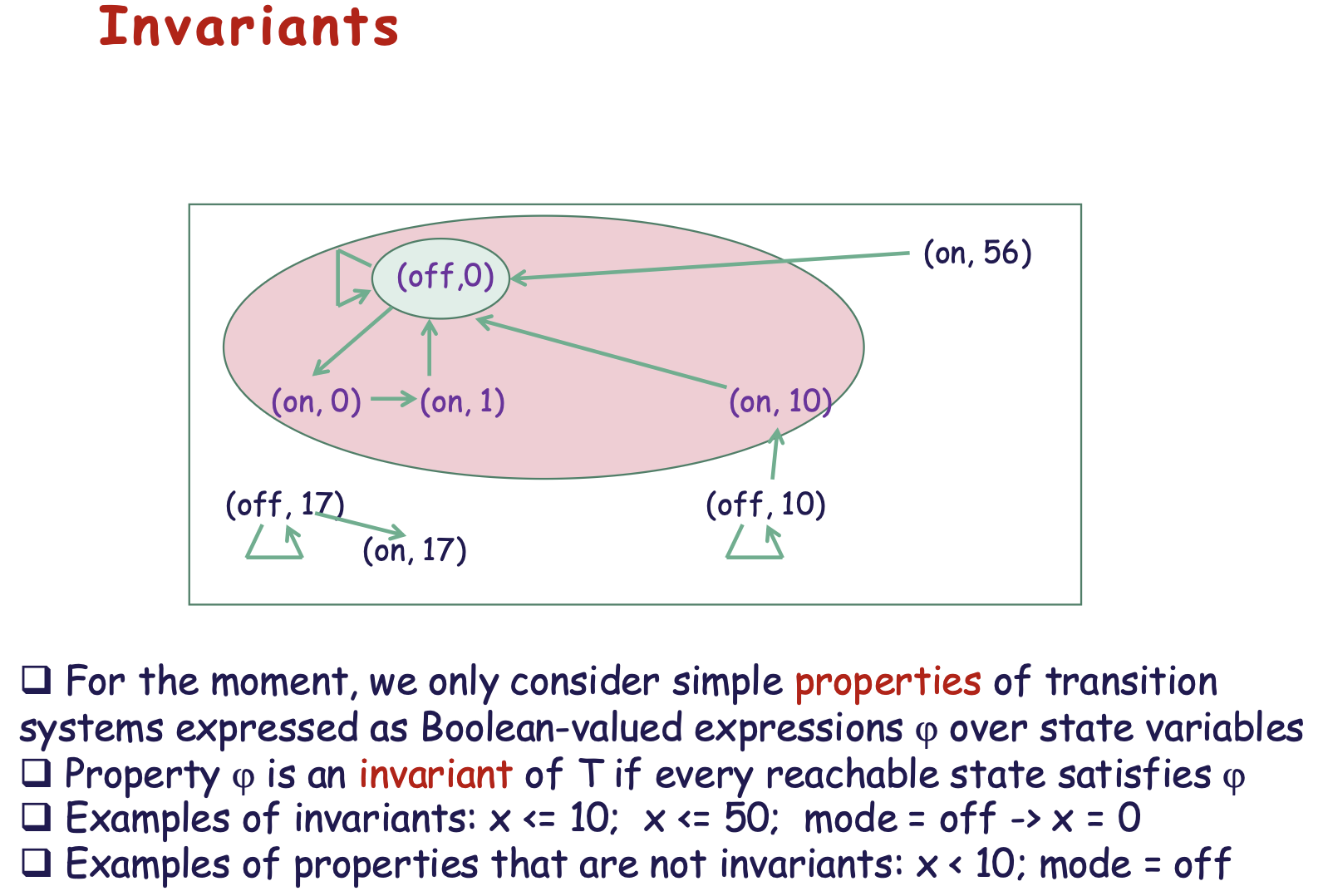 If “some machine” is an invariant, then the system is safe.
If “some machine” is an invariant, then the system is safe.
Example Formulas
(a) Universal Disjunction
{s₀ → s₁ → s₂ → ··· | ∀i : sᵢ ⊨ a ∨ b}
Meaning: Every state satisfies either property a or property b (or both)
- ∀i - for all positions i
- sᵢ ⊨ a ∨ b - state at position i satisfies a OR b
- Property type: Invariant and safety property (but not liveness)
(b) Historical Requirement
{s₀ → s₁ → s₂ → ··· | ∀i : sᵢ ⊨ b → ∃j ≤ i : sⱼ ⊨ a}
Meaning: Whenever b occurs, a must have occurred at some earlier or same position
- ∀i - for all positions i
- sᵢ ⊨ b → - if state i satisfies b, then…
- ∃j ≤ i : sⱼ ⊨ a - there exists some position j ≤ i where a holds
- Property type: Safety property (but not invariant or liveness)
(c) Future Guarantee
{s₀ → s₁ → s₂ → ··· | ∀i : sᵢ ⊨ a → ∃j ≥ i : sⱼ ⊨ b}
Meaning: Whenever a occurs, b must eventually occur at some future position
- ∀i - for all positions i
- sᵢ ⊨ a → - if state i satisfies a, then…
- ∃j ≥ i : sⱼ ⊨ b - there exists some position j ≥ i where b holds
- Property type: Liveness property (not safety, not invariant)
(d) Exact Count Constraint
{s₀ → s₁ → s₂ → ··· | |{i | sᵢ ⊨ a}| = 3}
Meaning: Exactly 3 states in the sequence satisfy property a
- |{i | sᵢ ⊨ a}| - cardinality (size) of the set of positions where a holds
- = 3 - equals exactly 3
- Property type: Neither safety nor liveness (intersection of both types)
(e) Conditional Liveness
{s₀ → s₁ → s₂ → ··· | (∀i ∃j > i : sⱼ ⊨ a) → (∀i ∃j > i : sⱼ ⊨ b)}
Meaning: If a occurs infinitely often, then b occurs infinitely often
- (∀i ∃j > i : sⱼ ⊨ a) - a occurs infinitely often (for every position, a occurs later)
- → - implies
- (∀i ∃j > i : sⱼ ⊨ b) - b occurs infinitely often
- Property type: Liveness property (not safety, not invariant)
(f) Eventual Stabilization
{s₀ → s₁ → s₂ → ··· | ∃i ∀j > i : sⱼ ⊭ a}
Meaning: Eventually, a stops occurring forever
- ∃i - there exists some position i such that…
- ∀j > i : sⱼ ⊭ a - for all positions j after i, a does not hold
- Property type: Liveness property (not safety, not invariant)
Quick Reference Table
| Symbol | Meaning | Type |
|---|---|---|
| ∀ | For all | Universal quantifier |
| ∃ | There exists | Existential quantifier |
| ⊨ | Satisfies/models | Satisfaction relation |
| ⊭ | Does not satisfy | Negated satisfaction |
| ∧ | AND | Logical conjunction |
| ∨ | OR | Logical disjunction |
| ¬ | NOT | Logical negation |
| → | Implies | Logical implication |
| U | Until | Temporal operator |
| |…| | Cardinality | Set size |